hàm số mũ hàm số lôgarit

By Admin 28/12/2023 0

Tổng hợp lí thuyết hàm số nón và hàm số lôgarit cộc gọn gàng, dễ dàng hiểu

Tổng phù hợp đề thi đua học tập kì 1 lớp 12 toàn bộ những môn

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa - GDCD

Bạn đang xem: hàm số mũ hàm số lôgarit

1. Định nghĩa

Hàm số nón là hàm số với dạng \(y = {a^x}\), hàm số lôgarit là hàm số với dạng  \(y = {\log _a}x\) ( với cơ số a dương không giống 1).

2. Tính hóa học của hàm số nón \(y = {a^x}\) \(( a > 0, a\ne 1)\).

- Tập xác định: \(\mathbb{R}\).

- Đạo hàm: \(∀x ∈\mathbb{R},y'= a^x \ln a\).

- Chiều biến hóa thiên          

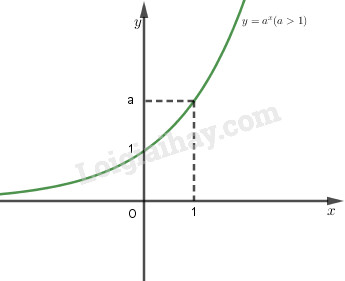
+) Nếu \(a> 1\) thì hàm số luôn luôn đồng biến

+) Nếu \(0< a < 1\) thì hàm số luôn luôn nghịch tặc biến

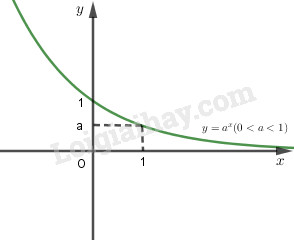
- Tiệm cận: trục \(Ox\) là tiệm cận ngang.

- Đồ thị ở trọn vẹn về phía bên trên trục hoành  \((y = {a^x} >0 \, \forall x)\), và luôn luôn rời trục tung bên trên điểm \(( 0;1)\) và trải qua điểm \((1;a)\).

3. Tính hóa học của hàm số lôgarit \(y = {\log _a}x\) \((a> 0, a\ne1)\).

- Tập xác định: \((0; +∞)\).

- Đạo hàm \(∀x ∈ (0; +∞),y'= \dfrac{1}{x\ln a}\).

- Chiều biến hóa thiên:  

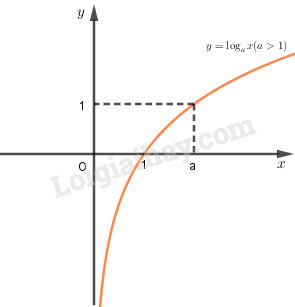
+) Nếu \(a> 1\) thì hàm số luôn luôn đồng biến

+) Nếu \(0< a < 1\) thì hàm số luôn luôn nghịch tặc biến

- Tiệm cận: Trục \(Oy\) là tiệm cận đứng.

- Đồ thị ở trọn vẹn phía phía bên phải trục tung, luôn luôn rời trục hoành bên trên điểm \((1;0)\) và trải qua điểm \((a;1)\).

Xem thêm: what do you do for a living

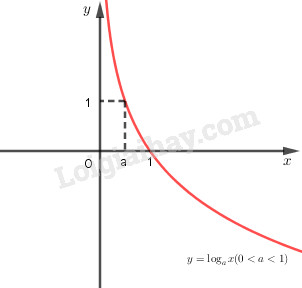
4. Chú ý 

- Nếu \(a > 1\) thì \(\ln a > 0\), suy đi ra \((a^x)'>0 \, \, \forall x\) và \({({\log_a}^x)}\; > 0,\;\;\forall x{\rm{ }} > 0;\) 

do cơ hàm số nón và hàm số lôgarit với cơ số to hơn 1 đều là những hàm số luôn luôn trực tiếp đồng biến hóa.

Tương tự động, nếu như \(0 < a< 1\) thì \(\ln a < 0\), \(({a^x})' < 0\) và \({({\log_a}^x)}\; < 0,\;\;\forall x{\rm{ }} > 0;\) ; hàm số nón và hàm số lôgarit với cơ số nhỏ rộng lớn 1 đều là những hàm số luôn luôn trực tiếp nghịch tặc biến hóa.

- Công thức đạo hàm của hàm số lôgarit hoàn toàn có thể không ngừng mở rộng thành

\( (\ln  |x|)'= \dfrac{1}{x}, ∀x \ne 0\) và \((\log _a|x|)' = \frac{1}{{x\ln a}},{\rm{ }}\forall x \ne 0.\)

Loigiaihay.com


Bình luận

Chia sẻ

>> Xem thêm

Xem thêm: cách tính giá trị biểu thức

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

>> Luyện thi đua TN trung học phổ thông & ĐH năm 2024 bên trên trang trực tuyến Tuyensinh247.com. Học từng khi, từng điểm với Thầy Cô giáo chất lượng tốt, không thiếu thốn những khoá: Nền tảng lớp 12; Luyện thi đua chuyên nghiệp sâu; Luyện đề đầy đủ dạng; Tổng ôn tinh lọc.