trung điểm của đoạn thẳng

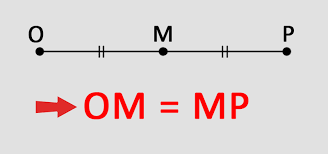
Khái niệm trung điểm của đoạn thẳng là 1 trong những điểm ở ở trung tâm đoạn trực tiếp và phân chia nó trở thành nhì đoạn trực tiếp có tính lâu năm đều nhau. Nếu tao gọi đoạn trực tiếp là AB và trung điểm của chính nó là M, thì đặc thù của trung điểm là MA = MB = AB/2. Như vậy tức là khoảng cách kể từ điểm M cho tới điểm A cũng vì chưng khoảng cách kể từ điểm M cho tới điểm B, và cả nhì khoảng cách này đều vì chưng 50% chừng lâu năm của đoạn trực tiếp AB. Trung điểm của đoạn trực tiếp còn được gọi là vấn đề ở trung tâm đoạn trực tiếp.

Bạn đang xem: trung điểm của đoạn thẳng

Trung điểm của đoạn trực tiếp là vấn đề ở ở trung tâm đoạn trực tiếp và phân chia đoạn trực tiếp trở thành nhì phần có tính lâu năm đều nhau. Nếu M là trung điểm của đoạn thẳng AB, thì tao đem MA = MB = AB/2. Trung điểm của đoạn trực tiếp còn được gọi là vấn đề chủ yếu.
Cách mò mẫm trung điểm của đoạn thẳng AB:
1. Tính chừng lâu năm đoạn trực tiếp AB bằng phương pháp dùng công thức khoảng cách Euclid: AB = sqrt((x2 - x1)^2 + (y2 - y1)^2).
2. Tìm tọa chừng trung điểm M bằng phương pháp lấy tầm nằm trong của tọa chừng nhì đầu mút của đoạn trực tiếp AB: M(x, y) = [(x1 + x2)/2, (y1 + y2)/2].
Ví dụ:
Cho đoạn trực tiếp với đầu mút A(1, 2) và B(5, 6).
Bước 1: Tính chừng lâu năm đoạn trực tiếp AB: AB = sqrt((5 - 1)^2 + (6 - 2)^2) = sqrt(16 + 16) = sqrt(32) = 4sqrt(2).
Bước 2: Tìm tọa chừng trung điểm M: M(x, y) = [(1 + 5)/2, (2 + 6)/2] = [3, 4].
Vậy trung điểm của đoạn thẳng AB là M(3, 4).

Trên một quãng trực tiếp, chỉ mất độc nhất một điểm là trung điểm. Trung điểm là vấn đề ở trung tâm của đoạn trực tiếp, phân chia đoạn trực tiếp bại trở thành nhì đoạn đem nằm trong chừng lâu năm.

Để xác lập trung điểm của một quãng trực tiếp, tất cả chúng ta hoàn toàn có thể tuân theo công việc sau:
Bước 1: Đặt thương hiệu cho tới nhì đầu mút của đoạn trực tiếp. Gọi nhì đặc điểm đó là A và B.
Bước 2: Sử dụng công thức tính trung điểm. Trung điểm của đoạn trực tiếp AB tiếp tục ở ở trung tâm nhì điểm A và B, và phân chia đoạn trực tiếp AB trở thành nhì đoạn có tính lâu năm đều nhau.
Công thức tính trung điểm là:
Trung điểm của đoạn trực tiếp AB = ((xA + xB) / 2, (yA + yB) / 2), vô bại (xA, yA) và (xB, yB) thứu tự là tọa chừng của điểm A và B.
Ví dụ: Nếu điểm A đem tọa chừng (2, 4) và điểm B đem tọa chừng (6, 8), tao hoàn toàn có thể tính được tọa chừng của trung điểm theo đòi công thức trên:
Trung điểm của đoạn trực tiếp AB = ((2 + 6) / 2, (4 + 8) / 2) = (4, 6).
Vậy, trung điểm của đoạn thẳng AB đem tọa chừng là (4, 6).

Trung điểm của đoạn trực tiếp ko nằm trong đường thẳng liền mạch bại. Trung điểm là 1 trong những điểm ở ở trung tâm đoạn trực tiếp và phân chia đoạn trực tiếp trở thành nhì đoạn có tính lâu năm đều nhau. Nó ko phía trên đường thẳng liền mạch nhưng mà chỉ phía trên phần vô của đoạn trực tiếp bại.

Xem thêm: điểm chuẩn đại học nha trang 2022

Trung điểm của đoạn trực tiếp được xem là điểm chủ yếu vì như thế nó đem một số trong những đặc thù đặc biệt quan trọng. Dưới đấy là một số trong những nguyên do khiến cho trung điểm được xem là điểm chính:
1. Đối xứng: Trung điểm của đoạn trực tiếp là vấn đề độc nhất ở ở trung tâm đoạn trực tiếp và phân chia đoạn trực tiếp trở thành nhì phần đều nhau. Như vậy tức là khi tao vẽ đường thẳng liền mạch trải qua trung điểm và tuy vậy song với đoạn trực tiếp thuở đầu, thì đường thẳng liền mạch này tiếp tục hạn chế đoạn trực tiếp trở thành nhì phần có tính lâu năm đều nhau. Như vậy tạo nên một sự đối xứng đẹp mắt so với đoạn trực tiếp và trung điểm.
2. Đối giao: Trung điểm của đoạn trực tiếp là vấn đề độc nhất nhưng mà những đường thẳng liền mạch vuông góc cho tới đoạn trực tiếp thuở đầu tiếp tục hạn chế qua loa. Nghĩa là, nếu như tao vẽ những đường thẳng liền mạch vuông góc cho tới đoạn trực tiếp kể từ nhì đầu của chính nó, thì những đường thẳng liền mạch này tiếp tục giao phó nhau đích bên trên trung điểm. Như vậy tạo nên một nút giao của những đường thẳng liền mạch vuông góc và đoạn trực tiếp, tăng tính đối giao phó và hài hòa và hợp lý của trung điểm.
3. Tính đẹp mắt và cân nặng đối: Trung điểm là vấn đề ở ở trung tâm đoạn trực tiếp, tạo nên một sự bằng phẳng và thích mắt vô hình học tập. Vị trí đặc biệt quan trọng của trung điểm hùn tạo nên một sự cân đối và sự phân bổ đồng đều của những phần của đoạn trực tiếp.
Tóm lại, trung điểm được xem là điểm chủ yếu của đoạn trực tiếp chính vì nó đem đặc thù đối xứng, đối giao phó và tạo nên sự bằng phẳng và thích mắt vô hình học tập.

Trong hình học tập, trung điểm của một quãng trực tiếp đem tầm quan trọng cần thiết như sau:
1. Chia đoạn trực tiếp trở thành nhì đoạn có tính lâu năm vì chưng nhau: Trung điểm của đoạn trực tiếp đó là điểm ở ở trung tâm nó. Việc phân chia đoạn trực tiếp trở thành nhì phần đều nhau hùn đơn giản nhận ra và đo lường trong số vấn đề hình học tập.
2. Tạo đường thẳng liền mạch đối xứng: Trung điểm của một quãng trực tiếp cũng chính là trung điểm của đường thẳng liền mạch chứa chấp đoạn bại. Từ bại, tao hoàn toàn có thể dùng trung điểm nhằm kiến thiết đường thẳng liền mạch đối xứng qua loa đoạn trực tiếp bại. Như vậy đặc biệt hữu ích trong công việc giải những vấn đề kha khá và xác lập những địa điểm đối xứng vô hình học tập.
3. Xác quyết định tọa độ: Khi biết tọa chừng nhì đầu mút của đoạn trực tiếp, tao hoàn toàn có thể đơn giản tính tọa chừng của trung điểm bằng phương pháp lấy tầm nằm trong của những tọa chừng của nhì đầu mút. Như vậy tạo điều kiện cho ta thuận tiện trong công việc nhận xét và đo lường những vấn đề về địa điểm vô không khí.
4. sít dụng trong số vấn đề hình học: Khái niệm trung điểm của đoạn thẳng được dùng thoáng rộng vô giải những vấn đề hình học tập cơ phiên bản và nâng lên. Nó là 1 trong những trong mỗi định nghĩa cơ phiên bản và cần thiết nhằm kiến thiết những vật chứng và lý giải cho những mệnh đề và quyết định lý vô hình học tập.
Nhờ tầm quan trọng cần thiết của chính nó, định nghĩa trung điểm của đoạn thẳng tạo điều kiện cho ta làm rõ rộng lớn về cấu tạo và đặc thù của những hình học tập trí thức và hoàn toàn có thể vận dụng nó trong công việc xử lý những vấn đề thực tiễn và trừu tượng.

Tính hóa học cơ phiên bản của trung điểm vô hình học tập là:
1. Nếu M là trung điểm của đoạn thẳng AB, thì chừng lâu năm của đoạn AM vì chưng chừng lâu năm của đoạn MB, cũng vì chưng 50% chừng lâu năm của đoạn AB.
2. Trung điểm của đoạn trực tiếp phân chia đoạn trực tiếp trở thành nhì đoạn có tính lâu năm đều nhau.
3. Điểm trung điểm của đoạn thẳng ở ở trung tâm nhì đầu mút của đoạn trực tiếp bại.
4. Khoảng cơ hội kể từ điểm trung điểm đến lựa chọn nhì đầu mút của đoạn trực tiếp là đều nhau.
Ví dụ: Giả sử đoạn trực tiếp AB có tính lâu năm là 10 đơn vị chức năng, và M là trung điểm của đoạn thẳng AB. Khi bại, chừng lâu năm của đoạn AM và đoạn MB tiếp tục đều là 5 đơn vị chức năng. Như vậy tức là điểm M nằm trong lòng điểm A và B, và phân chia đoạn AB trở thành nhì đoạn AM và MB có tính lâu năm đều nhau.

Trung điểm của đoạn trực tiếp phân chia đoạn trực tiếp trở thành những đoạn có tính lâu năm đều nhau, đích. Định nghĩa của trung điểm là vấn đề ở ở trung tâm đoạn trực tiếp và phân chia đoạn trực tiếp trở thành nhì đoạn có tính lâu năm đều nhau. Khi mang 1 đoạn trực tiếp AB và M là trung điểm của đoạn thẳng AB, tao đem MA = MB = AB/2. Như vậy tức là kể từ điểm M tới điểm A và kể từ điểm M tới điểm B đem nằm trong chừng lâu năm và chủ yếu vì chưng 50% chừng lâu năm của đoạn trực tiếp AB. Vì vậy, những đoạn trực tiếp được phân chia vì chưng trung điểm luôn luôn có tính lâu năm đều nhau.

Xem thêm: văn tả dòng sông quê em lớp 5 ngắn gọn

Trung điểm của đoạn trực tiếp có không ít phần mềm vô thực tiễn. Dưới đấy là một số trong những ví dụ về phần mềm của định nghĩa này:
1. Trung điểm vô technology thông tin:
- Trong nghành nghề hình đồ họa PC, trung điểm của một quãng trực tiếp là 1 trong những định nghĩa cần thiết muốn tạo rời khỏi cảm giác hoạt động mượt nhưng mà. Chẳng hạn, trong công việc dịch rời một hình hình ảnh từ vựng trí A cho tới địa điểm B bên trên màn hình hiển thị, tao hoàn toàn có thể dùng trung điểm của đoạn thẳng AB nhằm đo lường những địa điểm liên tiếp vô quy trình dịch rời, tạo nên cảm giác hoạt động mượt nhưng mà và thực tiễn rộng lớn.
2. Trung điểm vô phong cách thiết kế và xây dựng:
- Trung điểm của một cạnh vô tam giác hoàn toàn có thể được dùng nhằm vẽ những lối tầm, góc đối nhau đồng đẳng và những điểm bên trên những lối bại đem kỹ năng gắn kèm với vật tư kiến thiết. Như vậy đặc biệt hữu ích nhằm tăng tính bằng phẳng và đáp ứng sự ổn định quyết định na ná hợp lí vô kiến thiết và kiến thiết.
3. Trung điểm vô xác định và đo lường:
- Trong khối hệ thống xác định toàn thị trường quốc tế (GPS), những điểm trung điểm bên trên những đoạn trực tiếp hoàn toàn có thể được dùng nhằm xác xác định trí đúng mực của một đối tượng người dùng. phẳng cơ hội dùng vấn đề về trung điểm và khoảng cách của nhì điểm cuối của đoạn trực tiếp, tao hoàn toàn có thể đo lường địa điểm theo đòi những khối hệ thống xác định tọa chừng.
4. Trung điểm vô khoa học tập và kỹ thuật:
- Trung điểm của một quãng trực tiếp hoàn toàn có thể được dùng nhằm đo lường trọng tâm của một hình dạng phức tạp rộng lớn. phẳng cơ hội phân chia đoạn trực tiếp trở thành nhiều phần nhỏ, tao hoàn toàn có thể đo lường trung điểm của từng phần, tiếp sau đó phối hợp bọn chúng nhằm đo lường trọng tâm của toàn cỗ hình dạng.
Tóm lại, trung điểm của đoạn thẳng là 1 trong những định nghĩa cơ phiên bản vô hình học tập, tuy nhiên nó cũng có thể có nhiều phần mềm thực tiễn cần thiết vô nghành nghề technology vấn đề, phong cách thiết kế, xác định và thống kê giám sát, na ná vô khoa học tập và chuyên môn.