Bài tập Toán tính giá trị biểu thức thi học sinh giỏi lớp 5 Có đáp án

Bài tập dượt Tính độ quý hiếm biểu thức nâng lên lớp 5

Bài tập dượt Toán tính độ quý hiếm biểu thức nâng lên lớp 5 bao hàm những bài xích thói quen độ quý hiếm biểu thức trong những đề đua học viên chất lượng tốt lớp 5 với đáp án tất nhiên. Các bài xích tập dượt sau đây gom những em học viên ôn tập dượt với thủ tục bài xích hiệu suất cao nhất về dạng bài xích thói quen độ quý hiếm biểu thức ôn đua học viên chất lượng tốt, luyện đua Violympic đạt thành phẩm cao.

Bạn đang xem: tính giá trị biểu thức lớp 5

1. Cách giải dạng Toán Tính độ quý hiếm biểu thức

1. Biểu thức không tồn tại vệt ngoặc đơn chỉ mất phép tắc nằm trong và phép tắc trừ (hoặc chỉ mất phép tắc nhân và phép tắc chia) thì tao tiến hành những phép tắc tính theo đuổi trật tự kể từ ngược quý phái nên.

Ví dụ: 542 + 123 - 79 482 x 2 : 4

= 665 - 79 = 964 : 4

= 586 = 241

2. Biểu thức không tồn tại vệt ngoặc đơn, với những phép tắc tính nằm trong, trừ, nhân, phân chia thì tao tiến hành những phép tắc tính nhân, phân chia trước rồi tiến hành những phép tắc tính nằm trong trừ sau.

Ví dụ: 27 : 3 - 4 x 2

= 9 - 8

= 1

3. Biểu thức với vệt ngoặc đơn thì tao tiến hành những phép tắc tính nhập ngoặc đơn trước, những phép tắc tính ngoài vệt ngoặc đơn sau

Ví dụ: 25 x (63 : 3 + 24 x 5)

= 25 x (21 + 120)

=25 x 141

=3525

2. Bài tập dượt nâng lên Tính độ quý hiếm biểu thức lớp 5 với đáp án

Bài 1. a)Tính nhanh: $\frac{4678 \times 4679+4680 \times 31+4648}{4680 \times 4679-4678 \times 4679}$

b) Cho sản phẩm tính: 492 : 4 x 123 x 2 + 13 : 3

Hãy thêm thắt vệt ngoặc đơn nhập sản phẩm tính cơ sao mang lại thành phẩm là số ngẫu nhiên nhỏ nhất?

(Đề Vòng 1 - PGD Quảng Trạch, Quảng Bình năm học tập 1998 - 1999)

Giải

a) Tính nhanh:

$\frac{4678 \times 4679+4680 \times 31+4648}{4680 \times 4679-4678 \times 4679}$

$\begin{aligned} &=\frac{4678 \times 4679+(4679+1) \times 31+4648}{4679 \times(4680-4678)} \\ &=\frac{4678 \times 4679+4679 \times 31+31+4648}{4679 \times 2} \\ &=\frac{4678 \times 4679+4679 \times 31+4679}{4679 \times 2} \\ &=\frac{4679 \times(4678+31+1)}{4679 \times 2} \\ &=\frac{4679 \times 4710}{4679 \times 2}=\frac{4710}{2}=2355 \end{aligned}$

b) Cho sản phẩm tính: 492 : 4 x 123 x 2 + 13 : 3

Vậy để sở hữu thành phẩm nhỏ nhất tao nên sử dụng phép tắc phân chia, tao có: 492 (4 x 123) x (2 + 13) : 3

= 492 : 492 x 15 : 3

= 1 x 5 = 5

Bài 2. Viết những tổng sau kết quả của nhị quá số:

a) 242 + 286 + 66

b) 6767 + 5555 + 7878

(Đề Vòng 2 - PGD Quảng Trạch,Quảng Bình năm học tập 1998 - 1999)

Giải

Viết những tổng sau kết quả của nhị quá số:

a) 242 + 286 + 66

= 11 x 22 + 11 x 26 + 11 x 6

= 11 x (22 + 26 + 6)

= 11 x 54

b) 6767 + 5555 + 7878

= 67 x 101 + 55 x 101 + 78 x 101

= 101 x (67 + 55 + 78)

= 101 x 200

Bài 3. Tính nhanh:

a) 50 x 24,5 + 49 x 24,5 + 24,5

b) $\frac{7 \times 5 \times 12}{15 \times 8 \times 49}$

(Đề SGD Quảng Bình năm học tập 1998 - 1999)

Giải

Tính nhanh:

a) 50 x 24,5 + 49 x 24,5 + 24,5

= 24,5 x ( 50 + 49 + 1)

= 24,5 x 100 = 2450

$\begin{aligned} &=\frac{1 \times 1 \times 3}{3 \times 2 \times 7} \\ &=\frac{1}{14} \end{aligned}$

Bài 4. Cho biểu thức : A = (60 x 2 + 120 ) : 4

B = (30 x 4 + 120 ) : 8

Không tính độ quý hiếm tuy nhiên độ quý hiếm của biểu thức này to hơn, vì như thế sao?

(Đề PGD Quảng Trạch,Quảng Bình năm học tập 1999 - 2000)

Giải

Cho biểu thức : A = ( 60 x 2 + 120 ) : 4

B = ( 30 x 4 + 120 ) : 8

Vì: 60 x 2 = 30 x 4 nên số bị phân chia của nhị biểu thức tự nhau; số phân chia 4 < 8 vì thế A > B.

Bài 5. Tính độ quý hiếm biểu thức:

a) bằng phẳng 2 cách: ( 27,8 + 16,4 ) x 5

b) bằng phẳng cơ hội thời gian nhanh nhất: (792,81 x 0,25 + 792,81 x 0,75) x (11 x 9 – 900 x 0,1- 9)

(Đề SGD Quảng Bình năm học tập 1999 - 2000)

Giải

Tính độ quý hiếm biểu thức:

a) bằng phẳng nhị cách:

Cách 1: (27,8 + 16,4 ) x 5

= 44,2 x 5

= 221

Cách 2: (27,8 + 16,4 ) x 5

= 27,8 x 5 + 16,4 x 5

= 139 + 82

= 221

b) bằng phẳng cơ hội thời gian nhanh nhất:

(792,81 x 0,25 + 792,81 x 0,75) x (11 x 9 – 900 x 0,1- 9)

= 792,81 x ( 0,25 + 0,75) x ( 99 – 90 - 9)

= 792,81 x 1 x 0 = 0

Bài 6. a) Tính độ quý hiếm biểu thức: 0,86 x 4,21 + ( 5,79 : 10 ) x 0,86 – 3,8

b) Tính nhanh: (156,2 + 3,8 – 17,5 + 252,5 - 197) x ( 0,2 – 2 : 10) x 2001

(Đề PGD Quảng Trạch,Quảng Bình năm học tập 2000 - 2001)

Giải

a) Tính độ quý hiếm biểu thức:

0,86 x 4,21 + (57,9 : 10 ) x 0,86 – 3,8

= 0,86 x 4,21 + 5,79 x 0,86 – 3,8

= 0,86 x (4,21 + 5,79) – 3,8

= 0,86 x 10 – 3,8

= 8,6 – 3,8 = 4,8

Xem thêm: what do you do for a living

b) Tính nhanh:

(156,2 + 3,8 – 17,5 + 252,5 - 197) x (0,2 – 2 : 10) x 2001

= (156,2 + 3,8 – 17,5 + 252,5 - 197) x (0,2 – 0,2) x 2001

= (156,2 + 3,8 – 17,5 + 252,5 - 197) x 0 x 2001

= 0 ( Tích với 3 quá số với 1 quá số tự 0 nên tích tự 0)

Bài 7.

Câu 1: Tính thành phẩm rồi rút gọn gàng.

$\text { a) } \frac{5}{6}-\frac{3}{4}$

$\text { b) } \frac{4}{7}: \frac{2}{3}$

Câu 2: Tính độ quý hiếm biểu thức.

a) $\left(\frac{1}{2}-\frac{1}{3}+\frac{1}{5}\right):\left(\frac{1}{4}-\frac{1}{6}\right)$

b) $\left(100-\frac{2}{5}\right): \frac{4}{7}$

(Đề SGD Quảng Bình năm học tập 2000- 2001)

Giải

Câu 1: Tính thành phẩm rồi rút gọn gàng.

$\text { a) } \frac{5}{6}-\frac{3}{4}$

$\begin{aligned} &=\frac{20}{24}-\frac{18}{24} \\ &=\frac{2}{24}=\frac{1}{12} \end{aligned}$

$\text { b) } \frac{4}{7}: \frac{2}{3}$

$\begin{aligned} &=\frac{4}{7} \times \frac{3}{2} \\ &=\frac{12}{14}=\frac{6}{7} \end{aligned}$

Câu 2: Tính độ quý hiếm biểu thức.

a) $\left(\frac{1}{2}-\frac{1}{3}+\frac{1}{5}\right):\left(\frac{1}{4}-\frac{1}{6}\right)$

$\begin{aligned} &=\left(\frac{1}{6}+\frac{1}{5}\right): \frac{1}{12} \\ &=\frac{11}{30}: \frac{1}{12} \\ &=\frac{11}{30} \mathbf{x} \frac{12}{1}=\frac{22}{5}=4 \frac{2}{5} \end{aligned}$

b) $\left(100-\frac{2}{5}\right): \frac{4}{7}$

$\begin{aligned} &=\left(\frac{2500}{25}-\frac{2}{25}\right): \frac{4}{7} \\ &=\frac{2498}{25}: \frac{4}{7} \\ &=\frac{2498 \times 7}{25 \times 4}=\frac{17486}{100}=174,86 \end{aligned}$

Bài 8. Thực hiện nay tính độ quý hiếm biểu thức: 88 – 24 : 0,3 – ( 4,08 + trăng tròn,4 : 5 ) : 1,02

(Đề PGD Quảng Trạch,Quảng Bình năm học tập 2001 - 2002)

Giải

Thực hiện nay tính độ quý hiếm biểu thức:

88 – 24 : 0,3 – ( 4,08 + trăng tròn,4 : 5 ) : 1,02

= 88 – 80 – ( 4,08 + 4,08 ) : 1,02

= 8 – 8,16 : 1,02

= 8 – 8 = 0

Bài 9. Với 4 chữ số 2 và những phép tắc tính hãy lập những sản phẩm tính với thành phẩm theo thứ tự là:

0; 1; 2; 3; 4; 5; 6; 8; 9; 10

(Đề SGD Quảng Bình năm học tập 2001- 2002)

Giải

Ta có: (2 + 2) – (2+ 2) = 0

(2 + 2) : (2+ 2) = 1

( 2: 2) +( 2: 2 ) = 2

(2 x 2) – ( 2: 2) = 3

2 x 2 x 2 : 2 = 4

(2 x 2) + (2 : 2) = 5

2 x 2 x 2 - 2 = 6

(2 x 2 ) + (2 x 2) = 8

22 : 2 – 2 = 9

2 x 2 x 2 + 2 = 10

Bài 10. a) Tính độ quý hiếm biểu thức sau rồi kiểm tra độ quý hiếm cơ phân chia không còn mang lại những số này trong những số sau đây: 2; 3; 5.

(120 x 4 – 25 x 4) : (36 : 18)

b) Tính nhanh: $\mathrm{M}=\frac{88986 \times 2003-678}{88985 \times 2003+1325}$

(Đề PGD Quảng Trạch, Quảng Bình năm học tập 2002- 2003)

Giải

a) ( 120 x 4 – 25 x 4 ) : (36 : 18)

= 4 x ( 120 - 25) : 2

= 4 x 95 : 2 = 380 : 2 = 190

190 phân chia không còn mang lại 2 và 5 ko phân chia không còn mang lại 3

b) Tính nhanh:

$\mathrm{M}=\frac{88986 \times 2003-678}{88985 \times 2003+1325}$

$\begin{aligned} &M=\frac{(88985+1) \times 2003-678}{88985 \times 2003+1325} \\ &M=\frac{88985 \times 2003+2003-678}{88985 \times 2003+1325} \\ &M=\frac{88985 \times 2003+1325}{88985 \times 2003+1325}=1 \end{aligned}$

3. Bài tập dượt tự động luyện Tính độ quý hiếm biểu thức Toán lớp 5

Bài 1: Tính:

a. 70 - 49 : 7 + 3 x 6

b. 4375 x 15 + 489 x 72

c. (25915 + 3550 : 25) : 71

d. 14 x 10 x 32 : (300 + 20)

Bài 2: Tính:

a) (85,05 : 27 + 850,5) x 43 - 150,97

b) 0,51 : 0,17 + 0,57 : 1,9 + 4,8 : 0,16 + 0,72 : 0,9

Bài 3: Viết sản phẩm số với thành phẩm tự 100:

a) Với 5 chữ số 1.

b) Với 5 chữ số 5.

Bài 4: Cho sản phẩm tính: 128 : 8 x 16 x 4 + 52 : 4. Hãy thêm thắt vệt ngoặc đơn nhập sản phẩm tính cơ sao cho:

a) Kết ngược là nhỏ nhất với thể?

b) Kết ngược là lớn số 1 với thể?

Bài 5: Hãy điền thêm thắt vệt ngoặc đơn nhập biểu thức sau:

A = 100 - 4 x trăng tròn - 15 + 25 : 5

a) Sao mang lại A đạt độ quý hiếm lớn số 1 và độ quý hiếm lớn số 1 là bao nhiêu?

b) Sao mang lại A đạt độ quý hiếm nhỏ nhất và độ quý hiếm nhỏ nhất này là bao nhiêu?

Bài 6: Tìm độ quý hiếm số ngẫu nhiên của a nhằm biểu thức sau có mức giá trị nhỏ nhất , độ quý hiếm nhỏ nhất này là bao nhiêu?

A = (a - 30) x (a - 29) x …x (a - 1)

Bài 7: Tìm độ quý hiếm của số ngẫu nhiên a nhằm biểu thức sau có mức giá trị lớn số 1, độ quý hiếm lớn số 1 này là bao nhiêu?

A = 2006 + 720 : (a - 6)

Bài 8: Tính độ quý hiếm của biểu thức m x 2 + n x 2 + p x 2, biết:

a) m = 2006, n = 2007, p = 2008

b) m + n + p = 2009

Bài 9: Tính độ quý hiếm của biểu thức M, với a = 119 và b = 0, biết:

M = b: (119 x a + 2005) + (119 : a - b x 2005)

Bài 10: Tính độ quý hiếm biểu thức:

Xem thêm: bài tập về hiện tại đơn

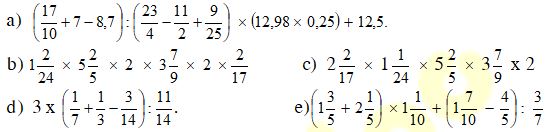
Tính độ quý hiếm biểu thức lớp 5

Các bài xích tập dượt về đề chính tính độ quý hiếm biểu thức khác:

Cách giải bài xích Toán tính thời gian nhanh độ quý hiếm của biểu thức
Bồi chăm sóc học viên chất lượng tốt môn Toán lớp 5: Biểu thức và phép tắc tính tương quan cho tới tính độ quý hiếm biểu thức

Bài tập dượt Toán tính độ quý hiếm biểu thức đua học viên chất lượng tốt lớp 5 là dạng Toán nâng lên nhập công tác phạm vi Toán nâng lên lớp 5 với những dạng bài xích tập dượt và đáp án cụ thể tất nhiên cho những em học viên lớp 4, lớp 5 gia tăng kỹ năng, không ngừng mở rộng những dạng Toán kể từ cơ phiên bản cho tới nâng lên. Hi vọng đó là tư liệu hữu ích cho những em học viên ôn đua học viên chất lượng tốt, ôn đua nhập lớp 6 hiệu suất cao. Chúc những em học tập chất lượng tốt.