Chủ đề Giải câu hỏi cho tới tam giác abc vuông tại a: Việc giải câu hỏi cho tới tam giác ABC vuông bên trên A là 1 bước cần thiết trong những việc học tập và hiểu về tam giác. Bài toán này gom tất cả chúng ta vận dụng những kỹ năng và công thức đo lường nhằm lần rời khỏi những độ quý hiếm của tam giác, kể từ cơ nâng lên kĩ năng toán học tập của tớ. Việc giải thành công xuất sắc câu hỏi này tiếp tục thực hiện cho tới tất cả chúng ta thấy hào hứng và thoải mái tự tin rộng lớn trong những việc học tập toán.
Cách giải câu hỏi cho tới tam giác ABC vuông bên trên A?
Để giải câu hỏi cho tới tam giác ABC vuông bên trên A, tất cả chúng ta rất có thể dùng những vấn đề đang được cho tới nhập đề bài bác nhằm lần những độ quý hiếm sót lại của tam giác.
Bước 1: Xác tấp tểnh những độ quý hiếm đang được cho:
- Đề bài bác cho thấy thêm tam giác ABC là tam giác vuông bên trên đỉnh A. Vấn đề này Có nghĩa là góc ABC là góc vuông (90 độ).
- Đường cao AH đang được cho tới và rất có thể dùng nhằm tính diện tích S của tam giác ABC.
Bước 2: Tính toán những độ quý hiếm còn lại:
- Để tính phỏng nhiều năm những cạnh của tam giác, tất cả chúng ta rất có thể dùng tấp tểnh lý Pythagoras hoặc những tỉ lệ thành phần nhập tam giác.
- Nếu biết nhị cạnh sót lại của tam giác (ví dụ AB và AC), tất cả chúng ta rất có thể dùng tỷ trọng đằm thắm bọn chúng nhằm tính những cạnh sót lại (vd: AB : AC = 3 : 4).
- Bên cạnh đó, cũng rất có thể dùng những hệ thức trigonometic, như sin, cos, tan nhằm đo lường những độ quý hiếm cần thiết lần.
Thêm nhập cơ, tất cả chúng ta cũng rất có thể dùng những quy tắc tấp tểnh lượng tam giác nhằm giải câu hỏi. Ví dụ: công thức Heron nhằm tính diện tích S của tam giác.
Tuy nhiên, nhằm giải câu hỏi ví dụ, cần phải biết rõ ràng những độ quý hiếm đang được cho tới và đòi hỏi ví dụ của đề bài bác.
Bạn đang xem: tam giác abc vuông tại a
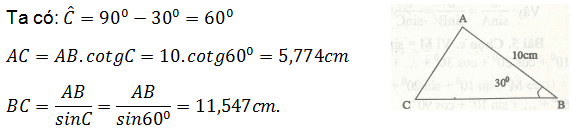
Tam giác ABC là tam giác vuông bên trên đỉnh A, với những cạnh AB = 5√3 centimet và AC = 5 centimet. Hãy tính phỏng nhiều năm cạnh BC của tam giác ABC.
Để tính phỏng nhiều năm cạnh BC của tam giác ABC, tớ rất có thể dùng tấp tểnh lý Pythagoras, một trong mỗi tấp tểnh lý cần thiết nhập hình học tập.
Theo tấp tểnh lý Pythagoras, nhập một tam giác vuông, bình phương của cạnh huyền (cạnh đối lập góc vuông) bởi tổng bình phương của nhị cạnh góc vuông.
Áp dụng nhập tam giác ABC, cạnh huyền là cạnh AB và cạnh góc vuông là cạnh AC. Ta có:
AB² = AC² + BC²
Thay những độ quý hiếm nhập phương trình, tớ có:
(5√3)² = 5² + BC²
75 = 25 + BC²
BC² = 75 - 25 = 50
Độ nhiều năm cạnh BC của tam giác ABC là căn bậc nhị của 50:
BC = √50 = √(25 x 2) = 5√2 cm
Vậy phỏng nhiều năm cạnh BC của tam giác ABC là 5√2 centimet.
Giải câu hỏi tam giác vuông ABC bên trên đỉnh A hiểu được cạnh AB = 6 centimet và BC = 8 centimet. Hỏi phỏng nhiều năm của cạnh AC là bao nhiêu?
Để giải câu hỏi này, tớ rất có thể vận dụng tấp tểnh lí Pytago nhập tam giác vuông. Định lí Pytago đem công thức: a^2 + b^2 = c^2, với a, b là phỏng nhiều năm 2 cạnh góc nhọn của tam giác vuông và c là phỏng nhiều năm cạnh huyền của tam giác vuông.
Vì tam giác ABC là tam giác vuông bên trên đỉnh A, tớ đem AB là cạnh huyền (cạnh ngược với góc vuông) và BC là cạnh góc nhọn. Đề bài bác cho thấy thêm AB = 6 centimet và BC = 8 centimet. Ta mong muốn lần phỏng nhiều năm cạnh AC.
Áp dụng công thức tấp tểnh lí Pytago, tớ có:
AC^2 = AB^2 + BC^2
AC^2 = 6^2 + 8^2
AC^2 = 36 + 64
AC^2 = 100
Để lần phỏng nhiều năm của cạnh AC, tớ tính căn bậc 2 của tất cả nhị phía của phương trình trên:
AC = √100
AC = 10
Vậy, phỏng nhiều năm của cạnh AC nhập tam giác ABC là 10 centimet.
Tam giác ABC là tam giác vuông bên trên đỉnh A và phỏng nhiều năm những cạnh AB và AC theo lần lượt là 3 centimet và 4 centimet. Tính phỏng nhiều năm cạnh BC của tam giác.
Để tính phỏng nhiều năm cạnh BC của tam giác ABC, tớ rất có thể dùng tấp tểnh lí Pythagoras. Định lí Pythagoras bảo rằng nhập một tam giác vuông, bình phương của cạnh huyền (BC) bởi tổng bình phương của 2 cạnh góc vuông (AB và AC). Vì vậy, tớ đem công thức sau:
BC^2 = AB^2 + AC^2
Với AB = 3 centimet và AC = 4 centimet, tớ rất có thể tính được BC như sau:
BC^2 = 3^2 + 4^2
BC^2 = 9 + 16
BC^2 = 25
Do cơ, nhằm tính phỏng nhiều năm BC, tiến hành căn bậc nhị bên trên cả nhị phía công thức:
BC = √25
BC = 5
Vậy phỏng nhiều năm cạnh BC của tam giác ABC là 5 centimet.
Tam giác ABC vuông bên trên A, đàng cao AH = 2, tính HB HC
Hãy coi video clip về tam giác ABC vuông bên trên A nhằm mày mò những đặc thù thú vị của tam giác đặc trưng này. Đây là 1 trong mỗi chủ thể thú vị nhập môn hình học tập và rất có thể khiến cho bạn luyện trí tuệ logic và tài năng giải quyết và xử lý những yếu tố phức tạp.
Cho tam giác vuông ABC bên trên đỉnh A, hiểu được cạnh AB = 10 centimet và góc ABC = 45 phỏng. Tính phỏng nhiều năm cạnh AC của tam giác.
Để tính phỏng nhiều năm cạnh AC của tam giác ABC, tớ rất có thể dùng tấp tểnh lí hạ tầng của tấp tểnh lí Pythagoras cho tới tam giác vuông :
Theo tấp tểnh lí Pythagoras, nhập một tam giác vuông, bình phương của phỏng nhiều năm cạnh huyền (cạnh đối lập góc vuông) bởi tổng bình phương của phỏng nhiều năm nhị cạnh góc vuông sót lại.
Với tam giác ABC, tớ đem cạnh AB = 10 centimet và góc ABC = 45 phỏng. Vì đó là một tam giác vuông bên trên đỉnh A, nên tớ lần phỏng nhiều năm cạnh BC.
Vì góc ABC = 45 phỏng, tớ có: BC^2 = AB^2 + AC^2.
Thay nhập đó: BC^2 = 10^2 + AC^2.
Vì tam giác vuông bên trên đỉnh A, nên tớ rất có thể dùng tấp tểnh lí Pythagoras nhằm lần phỏng nhiều năm cạnh BC. Ta có: BC = AB * sqrt(2).
Thay nhập đó: (AB * sqrt(2))^2 = 10^2 + AC^2.
Giải phương trình bên trên nhằm lần AC:
2 * 10^2 = 10^2 + AC^2.
200 = 100 + AC^2.
AC^2 = 200 - 100.
AC^2 = 100.
AC = sqrt(100).
AC = 10 centimet.
Vậy, phỏng nhiều năm cạnh AC của tam giác ABC là 10 centimet.
_HOOK_
Tam giác ABC là tam giác vuông bên trên đỉnh A và phỏng nhiều năm nhị cạnh AB và AC theo lần lượt là 12 centimet và 16 centimet. Hãy tính phỏng nhiều năm cạnh BC của tam giác.
Để tính phỏng nhiều năm cạnh BC của tam giác ABC, tớ rất có thể dùng tấp tểnh lý Pythagoras, tức là: \"Trong một tam giác vuông, bình phương của cạnh huyền bởi tổng bình phương của nhị cạnh góc vuông\". kề dụng tấp tểnh lý Pythagoras nhập tam giác ABC, tớ có:
AB^2 + AC^2 = BC^2
Thay độ quý hiếm AB = 12 centimet và AC = 16 centimet nhập công thức bên trên, tớ có:
12^2 + 16^2 = BC^2
144 + 256 = BC^2
400 = BC^2
Để lần cạnh BC, tớ cần thiết lấy căn bậc nhị của nhị vế phương trình trên:
√400 = √(BC^2)
Vì cạnh của tam giác ko thể có mức giá trị âm nên tớ chỉ lấy căn bậc nhị của số dương:
BC = trăng tròn cm
Do cơ, phỏng nhiều năm cạnh BC của tam giác ABC là trăng tròn centimet.
Cho tam giác ABC vuông bên trên đỉnh A và cạnh AB = 9 centimet, AC = 12 centimet. Tính phỏng nhiều năm cạnh BC của tam giác ABC.
Để tính phỏng nhiều năm cạnh BC của tam giác ABC, tớ rất có thể vận dụng tấp tểnh lý Pythagoras.
Theo tấp tểnh lý Pythagoras, nhập một tam giác vuông, bình phương của phỏng nhiều năm cạnh huyền (BC) bởi tổng bình phương của phỏng nhiều năm nhị cạnh góc vuông (AB và AC).
Với tam giác ABC vuông bên trên đỉnh A và cạnh AB = 9 centimet, AC = 12 centimet, tớ có:
BC^2 = AB^2 + AC^2
BC^2 = 9^2 + 12^2
BC^2 = 81 + 144
BC^2 = 225
Để lần phỏng nhiều năm cạnh BC, tớ lấy căn bậc nhị của tất cả nhị phía của phương trình:
BC = √225
BC = 15
Vậy phỏng nhiều năm cạnh BC của tam giác ABC là 15 centimet.
Xem thêm: sơ xuất hay sơ suất
Hình học tập 9 - Bài 1: Hệ thức lượng nhập tam giác vuông (mới nhất 2022)
Video về hình học tập 9 tiếp tục cho chính mình tầm nhìn tổng quan tiền về những kỹ năng cơ bạn dạng và cần thiết nhập môn hình học tập. Quý khách hàng sẽ tiến hành học tập về những mô hình học tập, kiểu vẽ và đo lường những đường thẳng liền mạch, góc, diện tích S và thể tích của những hình.
Toán lớp 9 | Hình 1: Hệ thức lượng nhập tam giác vuông
Học toán lớp 9 kể từ căn bạn dạng cho tới nâng lên trải qua video clip thú vị. Quý khách hàng tiếp tục mày mò những định nghĩa mới nhất, cơ hội giải những câu hỏi, và tập luyện kĩ năng đo lường. Đừng bỏ qua thời cơ nhằm nắm rõ kỹ năng toán 9 và nối tiếp thành công xuất sắc nhập học hành.
Tam giác ABC là tam giác vuông bên trên đỉnh A và hiểu được AB = 4 centimet và BC = 5 centimet. Tính phỏng nhiều năm cạnh AC của tam giác.
Để tính phỏng nhiều năm cạnh AC của tam giác ABC, tớ rất có thể dùng tấp tểnh lý Pythagoras. Định lý Pythagoras cho thấy thêm nhập một tam giác vuông, bình phương của phỏng nhiều năm cạnh huyền (cạnh đối lập góc vuông) bởi tổng bình phương của phỏng nhiều năm nhị cạnh góc vuông.
Áp dụng tấp tểnh lý Pythagoras nhập tam giác ABC, tớ có:
AC^2 = AB^2 + BC^2
Thay những độ quý hiếm đang được cho tới nhập công thức trên:
AC^2 = 4^2 + 5^2
AC^2 = 16 + 25
AC^2 = 41
Để lần phỏng nhiều năm cạnh AC, tớ cần thiết tính căn bậc nhị của 41:
AC = √41
Vậy, phỏng nhiều năm cạnh AC của tam giác ABC là căn bậc nhị của 41.
Tìm diện tích S tam giác ABC vuông bên trên đỉnh A hiểu được cạnh AB = 8 centimet và cạnh AC = 12 centimet.
Để giải câu hỏi này, tất cả chúng ta rất có thể dùng công thức tính diện tích S của tam giác vuông. Công thức này là S = một nửa * AB * AC. Ta đang được biết cạnh AB = 8 centimet và cạnh AC = 12 centimet. Thay nhập công thức, tất cả chúng ta có:
S = một nửa * 8 centimet * 12 cm
= 4 centimet * 12 cm
= 48 cm²
Vậy diện tích S tam giác ABC vuông bên trên đỉnh A là 48 cm².
Tam giác ABC là tam giác vuông bên trên đỉnh A và hiểu được phỏng nhiều năm cạnh AB gấp rất nhiều lần phỏng nhiều năm cạnh AC. Tính phỏng nhiều năm cạnh BC của tam giác.
Đầu tiên, tớ dùng tấp tểnh lý Pythagoras nhằm lần phỏng nhiều năm cạnh BC của tam giác vuông ABC. Định lý Pythagoras bảo rằng nhập một tam giác vuông, bình phương phỏng nhiều năm cạnh huyền (cạnh đối lập góc vuông) bởi tổng bình phương phỏng nhiều năm nhị cạnh góc vuông (cạnh kề góc vuông).
Giả sử cạnh AB có tính nhiều năm x centimet, vậy cạnh AC sẽ sở hữu phỏng nhiều năm là x/2 centimet, vì như thế theo đòi đề bài bác, phỏng nhiều năm cạnh AB gấp rất nhiều lần phỏng nhiều năm cạnh AC.
Áp dụng tấp tểnh lý Pythagoras, tớ có:
BC^2 = AB^2 - AC^2 = (x)^2 - (x/2)^2
= x^2 - (x^2)/4
= (4x^2 - x^2)/4
= 3x^2/4
Để lần phỏng nhiều năm cạnh BC, tớ tính căn bậc nhị của thành phẩm trên:
BC = √(3x^2/4)
= √(3/4) * √(x^2)
Xem thêm: Trang web VeBo TV - Xem live bóng đá hoàn toàn miễn phí
= (x√3) / 2
Vậy, phỏng nhiều năm cạnh BC của tam giác là (x√3) / 2 centimet.
_HOOK_
TOÁN 9- GIẢI TAM GIÁC VUÔNG đặc biệt hay
Đã lúc nào mình thích làm rõ rộng lớn về kiểu cách giải tam giác vuông? Video này tiếp tục khiến cho bạn thực hiện vấn đề đó. Quý khách hàng tiếp tục học tập về những công thức tính cạnh và diện tích S tam giác vuông, những đặc thù cần thiết và cơ hội vận dụng bọn chúng nhằm giải những câu hỏi tương quan.










Bình luận