đồ thị hàm bậc 3

Hàm số và loại thị là một trong những kiến thức và kỹ năng vô nằm trong cần thiết vô công tác Toán trung học tập hạ tầng. Vì vậy ngày hôm nay Kiến Guru xin được gửi đến độc giả nội dung bài viết về phần mềm của đồ thị hàm số bậc 3 trong các công việc giải những bài bác luyện toán. Đây là một trong những trong mỗi dạng thông thường xuất hiện nay ở những đề đua cuối cấp cho hao hao tuyển chọn sinh lên lớp 10. Cùng tìm hiểu thêm nhé:

Bạn đang xem: đồ thị hàm bậc 3

I. Đồ thị hàm số bậc 3 - Lý thuyết cơ bản

1. Các bước tham khảo hàm số bất kì.

Xét hàm y=f(x), nhằm tham khảo hàm số, tớ triển khai theo đòi công việc như sau:

• Tìm luyện xác lập.
• Xét sự đổi thay thiên:
• Tìm đạo hàm y’
• Tìm đi ra những điểm thực hiện y’=0 hoặc y’ ko xác lập.
• Xét vệt y’, kể từ cơ Kết luận chiều đổi thay thiên.

• Xác ấn định rất rất trị, mò mẫm số lượng giới hạn, vẽ bảng đổi thay thiên.
• Vẽ loại thị hàm số.

2. Khảo sát hàm số bậc 3.

Cho hàm số bậc 3 dạng:

• Tập xác định: D=R
• Sự đổi thay thiên
• Tính đạo hàm:
• Giải phương trình y’=0.
• Xét vệt y’, kể từ cơ suy đi ra chiều đổi thay thiên.
• Tìm số lượng giới hạn. Chú ý: hàm bậc thân phụ thưa riêng rẽ và những hàm nhiều thức thưa công cộng không tồn tại tiệm cận ngang và tiệm cận đứng. Sau cơ vẽ bảng đổi thay thiên.
• Vẽ loại thị: tớ mò mẫm những điểm đặc trưng nằm trong loại thị, thông thường là phú điểm của loại thị với trục tung, trục hoành.
• Khi phán xét, xem xét rằng đồ thị hàm bậc 3 nhận 1 điều thực hiện tâm đối xứng (là nghiệm của phương trình y’’=0), gọi là vấn đề uốn nắn của loại thị hàm số bậc 3.

Đăng Ký Học Ngay: Toán Thầy Thế 12 – Chuyên đề kiến thức và kỹ năng lớp 12

3. Dạng loại thị hàm số bậc 3:

Cho hàm số bậc 3 dạng:

Đạo hàm

Ta xẩy ra những tình huống mặt mày dưới:

• Phương trình y’=0 tồn bên trên nhị nghiệm phân biệt:

• Phương trình y’=0 đem nghiệm kép.

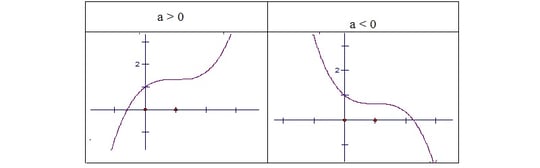
• Phương trình y’=0 vô nghiệm.

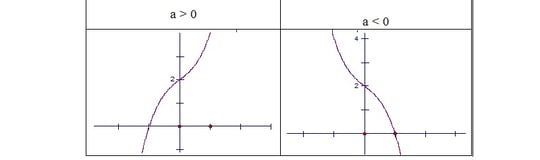
Ví dụ 1:  Khảo sát loại thị của hàm số bậc 3 sau: y=x³+3x²-4.

Hướng dẫn:

Bài này là một trong những bài bác tầm cỡ, nhằm tham khảo, thứu tự triển khai theo đòi những bước:

Tập xác định: D=R

Sự đổi thay thiên:

Tìm giới hạn: 

Vẽ bảng đổi thay thiên:

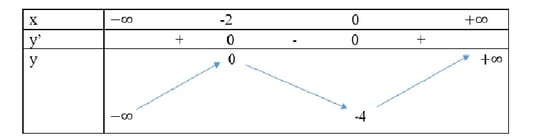
Hàm số đạt cực lớn bên trên x=-2, độ quý hiếm cực lớn y_CD=0

Hàm số đạt rất rất đái bên trên x=0, độ quý hiếm rất rất đái y_CT=-4

Vẽ loại thị:

Xác ấn định điểm đặc biệt: 

• Giao điểm của loại thị với trục hoành là nghiệm của phương trình hoành phỏng phú điểm y=0, hoặc

Vậy phú điểm với trục hoành là (-2;0) và (1;0)

• Giao điểm với trục tung: tớ thế x=0 vô hàm số hắn, được y=-4. 

Vậy phú điểm với trục tung là (0;-4).

• Điểm uốn:
  Vậy điểm uốn nắn của loại thị là (-1;-2)
  Ta nhận được loại thị sau:

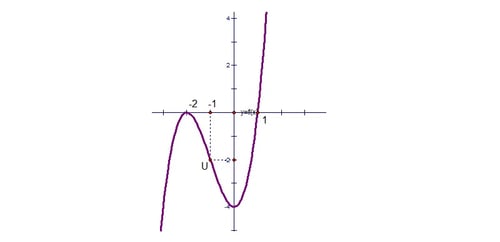
Nhận xét: cơ hội trình diễn bên trên phù phù hợp với những việc tự động luận, ngoại giả loại thị hàm số bậc 3 còn được dùng rộng thoải mái trong những việc trắc nghiệm nhưng mà ở cơ, yên cầu những kĩ năng nhận dạng một cơ hội nhanh gọn lẹ, đúng chuẩn nhằm mò mẫm đi ra đáp án việc.

Xem thêm: đại học tài chính marketing học phí

Ví dụ 2: Hãy mò mẫm hàm số đem loại thị là hình bên dưới đây:

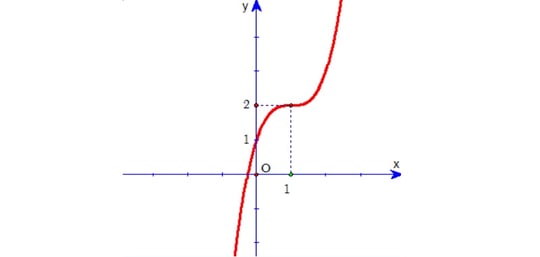
1. y=x³-3x+1
2. y=-x³+3x²+1
3. y=-x³+x²+3
4. y=x³-3x²+3x+1

Hướng dẫn:

Dựa vô dạng loại thị, tớ đem a>0. Hiển nhiên B, C bị loại bỏ.

Hàm số này không tồn tại rất rất trị, nên loại đáp án A.

Vậy đáp án D chính.

Nhận xét: việc này, những bạn cũng có thể lý luận theo đòi một cách tiếp, nhằm ý hàm số trải qua điểm (0;1), vậy loại đáp án C. Mặt không giống, loại thị trải qua (1;2) nên loại A, B. Vậy suy đi ra đáp án D chính.

Ví dụ 3: Cho hàm số bậc 3: có loại thị:

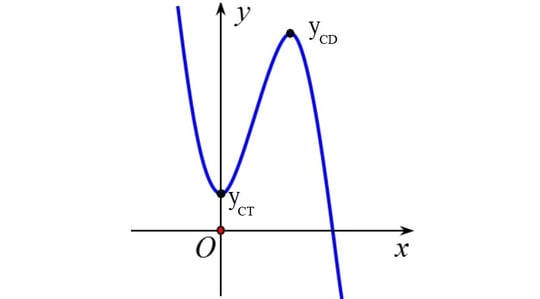
Tìm đáp án chủ yếu xác:

1. a<0, b>0, c>0, d>0.
2. a<0, b<0, c=0, d>0.
3. a>0, b<0, c>0, d<0.
4. a<0, b>0, c=0, d>0.

Hướng dẫn:

Từ hình vẽ loại thị, đơn giản dễ dàng nhận biết a<0.

Mặt không giống Lúc thay cho x=0, tớ đem y=d. Điểm (0;d) là phú của loại thị với trục tung, suy đi ra d>0.

Lại có: :

• Hàm số đạt rất rất đái bên trên x=0, nên y’(0)=0, suy đi ra c=0. Loại đáp án A.

lúc này y’=0, suy đi ra x=0 hoặc x=-2b/3a. Lại phụ thuộc vào loại thị, nhận biết hoành phỏng điểm cực lớn dương nên -2b/3a>0, kết phù hợp với a<0 suy đi ra b>0.

Vậy đáp án thực sự D.

Ví dụ 4: Cho hàm số . Xét 4 loại thị sau:

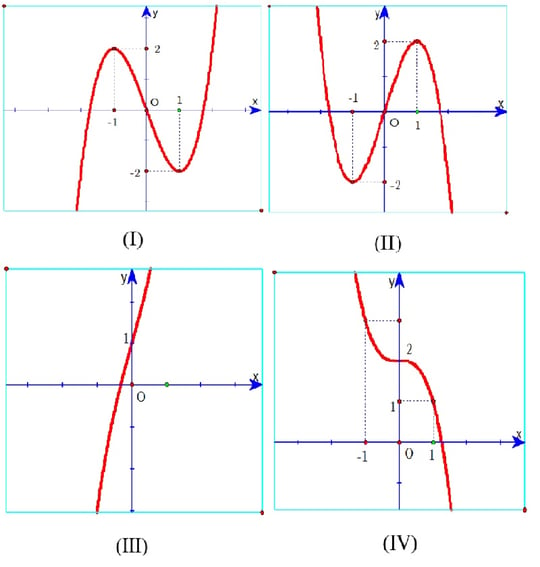
Hãy lựa lựa chọn mệnh đề chủ yếu xác:

1. Khi a>0 và f’(x)=0 đem nghiệm kép, loại thị hàm số được xem là (IV).
2. Khi a không giống 0 và f’(x)=0 tồn bên trên nhị nghiệm phân biệt thì loại thị (II) xẩy ra.
3. Đồ thị (I) Lúc a<0 và f’(x)=0 tồn bên trên nhị nghiệm phân biệt.
4. Đồ thị (III) Lúc a>0 và f’(x)=0 vô nghiệm.

Hướng dẫn:

Đồ thị (I) Lúc a>0, vậy loại C.

Đồ thị (II) Lúc a<0, vậy loại B vì thế ĐK a ở mệnh đề này sẽ không đầy đủ ngặt nghèo.

Đồ thị (III) xẩy ra Lúc a>0, f’(x)=0 vô nghiệm. 

Xem thêm: hình học không gian lớp 11

Đồ thị (IV) xẩy ra Lúc a<0, vậy loại A.

Kết thích hợp sự phân tách bên trên, D là đáp án đúng chuẩn.

Trên đó là tổ hợp của Kiến Guru về đồ thị hàm số bậc 3. Hy vọng trên đây được xem là tư liệu ôn luyện có lợi cho chính mình phát âm trong những kì đua tiếp đây. Đồng thời, Lúc phát âm hoàn thành nội dung bài viết, những các bạn sẽ vừa vặn gia tăng lại kiến thức và kỹ năng của bạn dạng thân mật, hao hao tập luyện được trí tuệ giải toán về loại thị hàm số. Học luyện là không ngừng nghỉ ngủ, những bạn cũng có thể tìm hiểu thêm tăng những nội dung bài viết có lợi không giống bên trên trang của Kiến Guru nhé. Chúc chúng ta học hành thiệt tốt!