cho tam giác abc nội tiếp đường tròn tâm o

Trong lịch trình học tập toán lớp 9, bài tập dượt chứng tỏ tam giác nội tiếp lối tròn trĩnh hoặc bài bác tập dượt chứng tỏ lối tròn trĩnh nước ngoài tiếp tam giác là bài bác ăn được điểm trong mỗi đề đánh giá. Các em học viên chỉ việc cầm có thể lý thuyết, gọi kỹ đề bài bác là rất có thể xử lý vấn đề một cơ hội đơn giản. Dưới phía trên được xem là những kỹ năng và kiến thức về tam giác nội tiếp lối tròn trĩnh và bài bác tập dượt áp dụng tương quan tuy nhiên HOCMAI mong muốn đem tới những em.

I. Lý thuyết về tam giác nội tiếp lối tròn

1. Khái niệm

Một tam giác sở hữu 3 đỉnh phía trên một lối tròn trĩnh được gọi là tam giác nội tiếp lối tròn trĩnh (hay lối tròn trĩnh này là lối tròn trĩnh nước ngoài tiếp tam giác)

Bạn đang xem: cho tam giác abc nội tiếp đường tròn tâm o

Ví dụ:

Cho tam giác ABC, sở hữu 3 đỉnh A, B, C nằm trong phía trên một lối tròn trĩnh tâm I

Vậy tam giác ABC là tam giác nội tiếp lối tròn trĩnh tâm I

Hoặc lối tròn trĩnh tâm I là lối tròn trĩnh nước ngoài tiếp tam giác ABC

2. Định lý

Bất kỳ một tam giác nào là cũng có thể có một lối tròn trĩnh nước ngoài tiếp.

3.Xác toan tâm của lối tròn trĩnh nước ngoài tiếp tam giác

• Tâm của lối tròn trĩnh nước ngoài tiếp tam giác là phó điểm của phụ thân lối trung trực của phụ thân cạnh nhập tam giác.
• Trong tam giác vuông, trung điểm cạnh huyền đó là tâm của lối tròn trĩnh nước ngoài tiếp tam giác vuông ấy.
• Trong tam giác đều, tâm lối tròn trĩnh nước ngoài tiếp và nội tiếp tam giác trùng cùng nhau.

Bài 1: Cho tam giác ABC nước ngoài tiếp lối tròn trĩnh tâm O, khi bại tao sở hữu những lối trung trực OD, OE, OF theo lần lượt vuông góc bên trên tủng điểm của những cạnh AB, AC và BC như hình mặt mũi dưới:

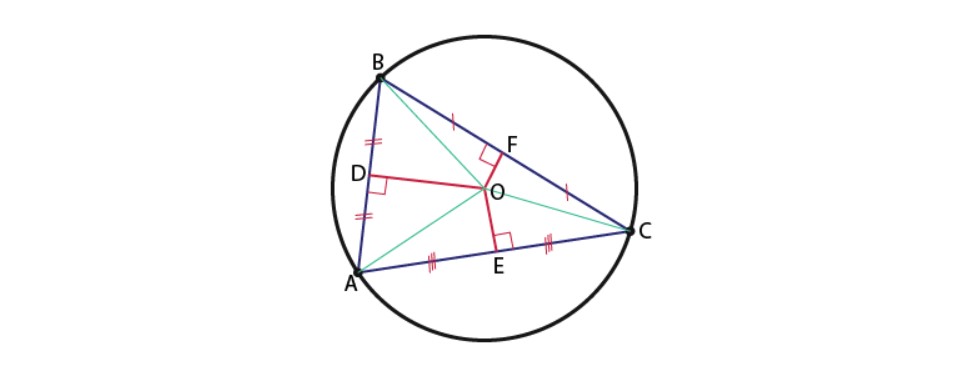
Hướng dẫn giải:

Nhìn hình vẽ tao thấy: những lối phân giác ứng là OB, OA và OC.

Xét tam giác OAB, tao có:

OD là lối trung trực bên trên cạnh AB, AD = DB

Tam giác ODA = tam giác ODB

OA = OB (1)

Xét tam giác OAC, tao có:

OE là lối trung trực bên trên cạnh AC, AE = EC

tam giác OEA = tam giác OEC

OA = OC (2)

Gọi r là nửa đường kính lối tròn trĩnh nước ngoài tiếp tâm O

Tứ (1) và (2) suy ra: r = OB = OA = OC (3)

Xem thêm: niềm tin là gì nlxh

Tiếp theo dõi tao cần thiết chứng tỏ khoảng cách kể từ O cho tới những cạnh tam giác ABC nhỏ rộng lớn bán kính r.

Gọi điểm M ngẫu nhiên phía trên cạnh AD, tao có:

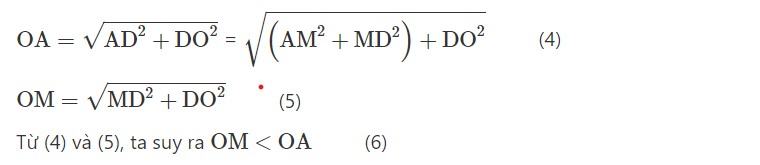
Từ bại suy rời khỏi khoảng cách kể từ tâm O cho tới những cạnh của tam giác ABC nhỏ rộng lớn nửa đường kính r của lối tròn trĩnh.

Từ (3) và (6), tao sở hữu lối tròn trĩnh tâm O là lối tròn trĩnh nước ngoài tiếp tam giác ABC (điều cần thiết triệu chứng minh)

Bài 2: Hãy triệu chứng minh:

a. Tâm của lối tròn trĩnh nước ngoài tiếp tam giác là trung điểm của cạnh huyền thì tam giác này là tam giác vuông.

b. Nếu một tam giác sở hữu một cạnh là 2 lần bán kính của lối tròn trĩnh nước ngoài tiếp thì tam giác này là tam giác vuông.

Hướng dẫn giải:

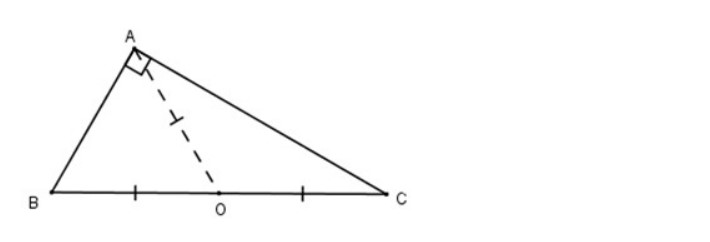
b. Xét tam giác ABC nội tiếp lối tròn trĩnh tâm O 2 lần bán kính BC.

Ta có: OA = OB = OC = r

Suy rời khỏi OA = 50% BC 

do bại tam giác ABC vuông bên trên A (dựa theo dõi đặc thù lối trung tuyến nhập tam giác vuông)

Bài 3: Nối dù ở cột trái ngược với dù ở cột cần sao mang lại mến hợp:

Hướng dẫn giải: (1) – (5), (2) – (6), (3) – (4).

Bài 4: Cho tam giác ABC nội tiếp lối tròn trĩnh tâm C, tia phân giác của góc BAC rời lối tròn trĩnh bên trên M. Tạo lối cao AH. Hãy triệu chứng minh:

a. M là trung điểm của thừng BC

b. AM là tia phân giác của góc OAH.

Hướng dẫn giải:

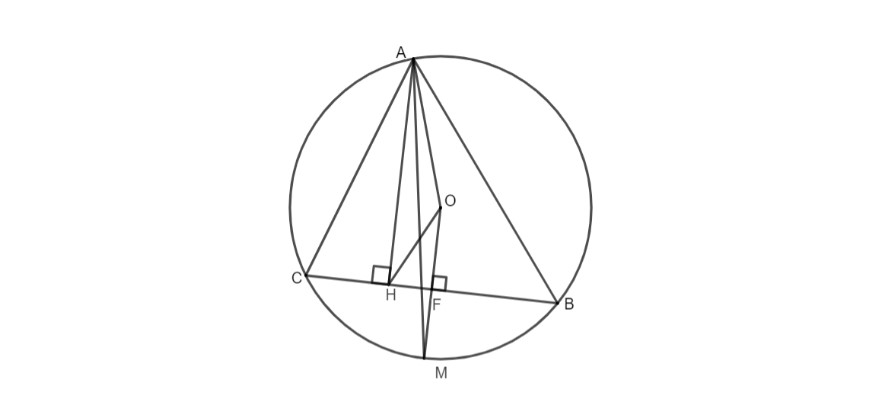
Xem thêm: nước việt nam nằm ở

Kiến thức cơ phiên bản liên quan:

• Khái niệm góc nội tiếp
• Khái niệm tứ giác nội tiếp
• Bài tập dượt hệ thức viet

Trên đấy là kỹ năng và kiến thức căn phiên bản và những bài tập dượt chứng tỏ tam giác nội tiếp. Để nắm vững kỹ năng và kiến thức rộng lớn, những em học viên hãy lần thiệt nhiều bài bác tập dượt không giống nhằm ôn luyện nhé. Cảm ơn những em vẫn gọi nội dung bài viết này và nhớ là truy vấn nhập trungtamtoiec.edu.vn để sở hữu thêm vào cho bản thân nhiều kỹ năng và kiến thức có ích nữa đấy.