Chủ đề hình chops tứ giác đều: Hình chóp tứ giác đều là 1 hình trạng chóp đặc trưng, mang tới sự rất dị và thích mắt. Với lòng hình vuông vắn và lối cao trải qua tâm lòng, hình chóp này đưa đến một design phù hợp và vô trẻo. Với tính đều, hình chóp tứ giác đều gom gia tăng sự bằng vận và thường xuyên vô không khí, thú vị sự lưu ý và tạo nên điểm vượt trội mang lại ngẫu nhiên không khí này.
Hình chóp tứ giác đều là gì?
Hình chóp tứ giác đều là 1 mô hình chóp đem Điểm sáng lòng là 1 hình vuông vắn và lối cao của chóp trải qua tâm của hình vuông vắn (đi qua loa phó của hai tuyến đường chéo cánh của hình vuông). Điểm đặc trưng của mô hình chóp này là toàn bộ những cạnh mặt mũi đều phải sở hữu nằm trong chừng nhiều năm và toàn bộ những góc đều giống hệt.
Để xác lập một hình chóp tứ giác đều, tất cả chúng ta hoàn toàn có thể tuân theo quá trình sau:
Bước 1: Vẽ một hình vuông vắn thực hiện lòng mang lại chóp.
Bước 2: Vẽ lối chéo cánh của hình vuông vắn.
Bước 3: Vẽ đường thẳng liền mạch kể từ tâm lòng của hình vuông vắn cho tới đỉnh chóp.
Bước 4: Kiểm tra coi những cạnh mặt mũi đem nằm trong chừng nhiều năm ko và những góc của những tam giác mặt mũi đem đều bằng nhau ko. Nếu cả nhị ĐK đều đích, thì phía trên đó là một hình chóp tứ giác đều.
Ví dụ, tớ mang trong mình một hình chóp tứ giác đều đem lòng là hình vuông vắn với từng cạnh nhiều năm 4cm. Đường cao của chóp trải qua tâm của hình vuông vắn và có tính nhiều năm 5cm. Ta hoàn toàn có thể xác lập đấy là một hình chóp tứ giác đều bằng phương pháp đánh giá coi những cạnh mặt mũi đem nằm trong chừng nhiều năm ko và những tam giác mặt mũi đem nằm trong góc ko.
Bạn đang xem: hình chóp tứ giác đều
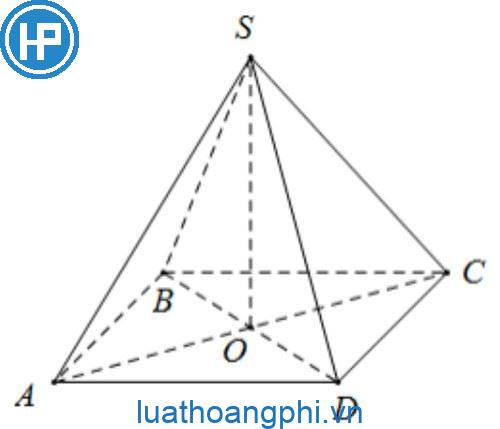

Hình chóp tứ giác đều phải sở hữu Điểm sáng gì?
Hình chóp tứ giác đều phải sở hữu những Điểm sáng sau:
1. Đáy của chóp là 1 hình vuông: Đáy của chóp tứ giác đều là 1 hình vuông vắn, tứ giác này còn có chừng nhiều năm những cạnh đều bằng nhau và những góc nội tiếp đều vày 90 chừng.
2. Các mặt mũi mặt của chóp là những tam giác cân nặng đều nhau: Các mặt mũi mặt của chóp tứ giác túc tắc là những tam giác cân nặng, tức là những cạnh của tam giác có tính nhiều năm đều bằng nhau và những góc nhị đỉnh cạnh mặt mũi đều đều bằng nhau.
3. Các mặt mũi mặt và lòng đều hạn chế nhau vuông góc: Các mặt mũi mặt và lòng của chóp tứ giác đều hạn chế nhau vuông góc, tức là lối cao của chóp trải qua tâm lòng, tức là phó của hai tuyến đường chéo cánh của hình vuông vắn lòng.
4. Đỉnh của chóp phía trên lối trục đối xứng của hình vuông vắn đáy: Đỉnh của chóp tứ giác đều phía trên lối trục đối xứng của hình vuông vắn lòng, tức tà tà tâm lòng, phó điểm của hai tuyến đường chéo cánh của hình vuông vắn lòng.
Những Điểm sáng này khái niệm một hình chóp tứ giác đều và nếu như một hình chóp đáp ứng nhu cầu được những Điểm sáng này thì nó được xem như là hình chóp tứ giác đều.
Làm sao nhằm xác lập một hình chóp tứ giác đều?
Để xác lập một hình chóp tứ giác đều, tất cả chúng ta cần thiết tuân theo quá trình sau đây:
Bước 1: Kiểm tra coi lòng của chóp đem nên là 1 hình vuông vắn ko. Nếu lòng là hình vuông vắn, tất cả chúng ta tổ chức lịch sự Cách 2. Nếu ko, chóp ko nên là 1 hình chóp tứ giác đều.
Bước 2: Xác ấn định những lối chéo cánh của hình vuông vắn lòng. Đường chéo cánh là lối nối nhị đỉnh ko kề nhau của hình vuông vắn. Gọi hai tuyến đường chéo cánh là AC và BD.
Bước 3: Vẽ đường thẳng liền mạch trải qua tâm lòng của hình vuông vắn và hạn chế những đỉnh của hình chóp. Đường trực tiếp này được xem là lối cao của chóp và tất cả chúng ta gọi nó là EF.
Bước 4: Kiểm tra coi lối cao EF đem trải qua phó điểm của hai tuyến đường chéo cánh AC và BD hay là không. Nếu EF trải qua phó điểm của AC và BD, tất cả chúng ta hoàn toàn có thể Tóm lại rằng đấy là một hình chóp tứ giác đều. trái lại, nếu như EF ko trải qua phó điểm của AC và BD, chóp ko nên là tứ giác đều.
Lưu ý: Khi xác lập một hình chóp tứ giác đều, tất cả chúng ta cũng cần được đánh giá những mặt mũi mặt của chóp nhằm đảm nói rằng bọn chúng là những tam giác cân nặng và đem đỉnh chung (đỉnh của chóp).
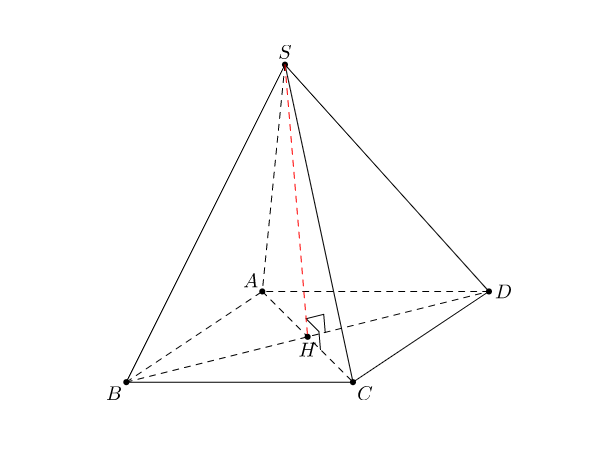
Công thức tính diện tích S mặt mũi mặt của hình chóp tứ giác đều là gì?
Công thức tính diện tích S mặt mũi mặt của hình chóp tứ giác đều là mặt phẳng lòng nhân với độ cao và phân tách song. Để tính diện tích S mặt mũi mặt mũi, tớ đem quá trình sau:
1. Xác ấn định lòng của hình chóp: Hình chóp tứ giác đều phải sở hữu lòng là 1 hình vuông vắn. Đoạn trực tiếp AB, BC, CD, DA là những cạnh của hình vuông vắn lòng.
2. Tính toán độ cao của hình chóp: Chiều cao của hình chóp tứ giác đều là lối cao trải qua tâm lòng và đem hai con mắt bên trên điểm X, nút giao của hai tuyến đường chéo cánh của hình vuông vắn lòng. Đoạn trực tiếp AX là độ cao của hình chóp.
3. Tính diện tích S mặt mũi đáy: Diện tích mặt mũi lòng của hình chóp tứ giác đều là diện tích S hình vuông vắn lòng. Để tính diện tích S hình vuông vắn, tớ đem công thức S = a^2, vô bại liệt a là cạnh của hình vuông vắn lòng.
4. Tính diện tích S mặt mũi bên: Diện tích mặt mũi mặt của hình chóp tứ giác đều vày nửa tích diện tích S mặt mũi lòng và độ cao. Công thức tính diện tích S mặt mũi mặt là S_ben = (1/2) * S_d = (1/2) * a^2 * h, vô bại liệt S_ben là diện tích S mặt mũi mặt mũi, S_d là diện tích S mặt mũi lòng, a là cạnh hình vuông vắn lòng và h là độ cao của hình chóp.
Với những độ quý hiếm a và h tiếp tục biết, tớ hoàn toàn có thể tính được diện tích S mặt mũi mặt của hình chóp tứ giác đều theo dõi công thức bên trên.
Cách tính diện tích S toàn phần của hình chóp tứ giác đều?
Để tính diện tích S toàn phần của hình chóp tứ giác đều, tất cả chúng ta hoàn toàn có thể dùng công thức sau:
Diện tích toàn phần = diện tích S lòng + tổng diện tích S những mặt mũi bên
1. Diện tích đáy: Vì hình chóp tứ giác đều đem lòng là hình vuông vắn, nên diện tích S lòng tiếp tục vày cạnh căn bậc nhị.
Điều bại liệt Có nghĩa là nếu như cạnh lòng là a, thì diện tích S lòng được xem là a^2.
2. Diện tích từng mặt mũi bên: Hình chóp tứ giác đều phải sở hữu tổng số 4 mặt mũi mặt là những tam giác cân nặng. Để tính diện tích S từng mặt mũi mặt mũi, tất cả chúng ta nên biết những cạnh của tam giác và độ cao của tam giác.
Đặt a là cạnh của lòng (tương tự động với cạnh của tam giác cân), và h là độ cao của tam giác.
Áp dụng công thức diện tích S tam giác, diện tích S từng mặt mũi mặt tiếp tục vày (1/2) * a * h.
3. Tổng những mặt mũi bên: Vì hình chóp tứ giác đều đem 4 mặt mũi mặt là những tam giác cân nặng, nên tổng diện tích S những mặt mũi mặt được xem là 4 phiên diện tích S từng mặt mũi mặt mũi.
4. Tính tổng diện tích S toàn phần: Để tính tổng diện tích S toàn phần, tất cả chúng ta nằm trong diện tích S lòng và tổng diện tích S những mặt mũi mặt mũi.
Tổng diện tích S toàn phần = diện tích S lòng + tổng diện tích S những mặt mũi mặt = a^2 + 4 * (1/2) * a * h = a^2 + 2 * a * h.
Vậy, phương pháp tính diện tích S toàn phần của hình chóp tứ giác đều là a^2 + 2 * a * h.
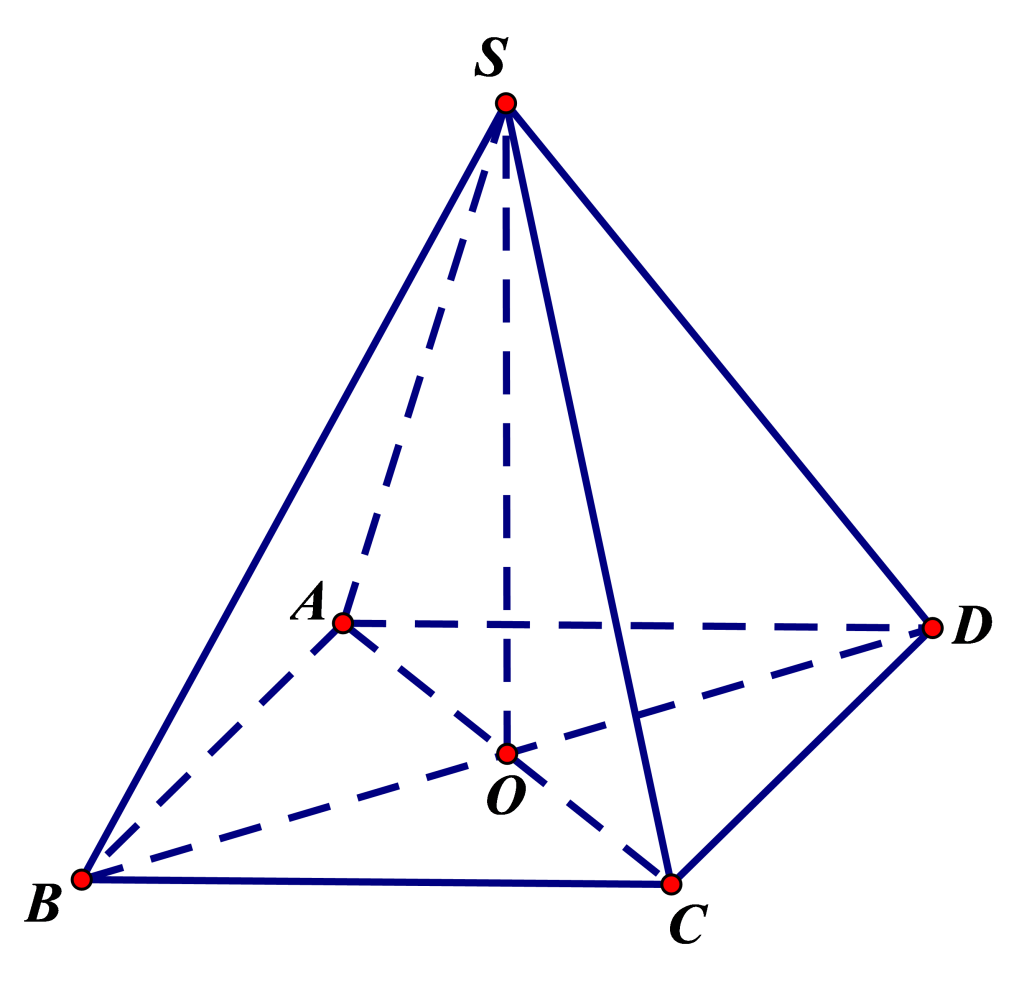
_HOOK_
Xem thêm: việc giải quyết vấn đề năng lượng ở bắc trung bộ chủ yếu dựa vào
TOÁN 8 - HÌNH CHÓP TỨ GIÁC ĐỀU - THẦY KENKA
Xem đoạn phim về hình chóp tứ giác đều nhằm mày mò công thức đo lường và những đặc thù rất dị của chính nó. Nhờ bại liệt, các bạn sẽ nhanh gọn lẹ hiểu về hình học tập và hoàn toàn có thể vận dụng vô giải những vấn đề phức tạp.
CÔNG THỨC TÍNH NHANH THỂ TÍCH KHỐI CHÓP TỨ GIÁC ĐỀU
Bạn mong muốn tính nhanh chóng những đại lượng vô hình chóp? Xem ngay lập tức đoạn phim về công thức tính nhanh chóng, được lý giải một cơ hội giản dị và đơn giản và dễ dàng nắm bắt. Sẽ rất rất hữu ích mang lại những vấn đề về hình chóp tuy nhiên các bạn đang được gặp gỡ nên.
Hãy cho biết thêm phương pháp tính thể tích của hình chóp tứ giác đều?
Để tính thể tích của hình chóp tứ giác đều, tớ dùng công thức sau:
V = 1/3 × A_b × H
Trong đó:
- V là thể tích của hình chóp.
- A_b là diện tích S lòng hình chóp.
- H là chừng nhiều năm lối cao của hình chóp.
Bước 1: Tính diện tích S lòng hình chóp.
Diện tích lòng hình chóp tứ giác đều là diện tích S của một hình vuông vắn. Để tính diện tích S hình vuông vắn, tớ đem công thức:
A_b = a^2
Trong bại liệt, a là cạnh của hình vuông vắn.
Bước 2: Tính chừng nhiều năm lối cao của hình chóp.
Để tính chừng nhiều năm lối cao của hình chóp tứ giác đều, tớ dùng công thức:
H = a × √2 / 2
Trong bại liệt, a là cạnh của lòng hình chóp.
Bước 3: Tính thể tích của hình chóp.
Sau Lúc tính được diện tích S lòng và chừng nhiều năm lối cao của hình chóp, tớ vận dụng công thức:
V = 1/3 × A_b × H
Thực hiện tại những luật lệ tính nhằm đo lường độ quý hiếm thể tích.
Hy vọng những vấn đề bên trên tiếp tục khiến cho bạn hiểu phương pháp tính thể tích của hình chóp tứ giác đều.
Hình chóp tứ giác đều phải sở hữu từng nào mặt?
Hình chóp tứ giác đều phải sở hữu tổng số 5 mặt mũi. Mặt lòng của chóp là 1 hình vuông vắn và mặt mũi mặt của chóp là tứ tam giác đều. Như vậy, hình chóp tứ giác đều có một mặt mũi lòng và 4 mặt mũi mặt mũi.
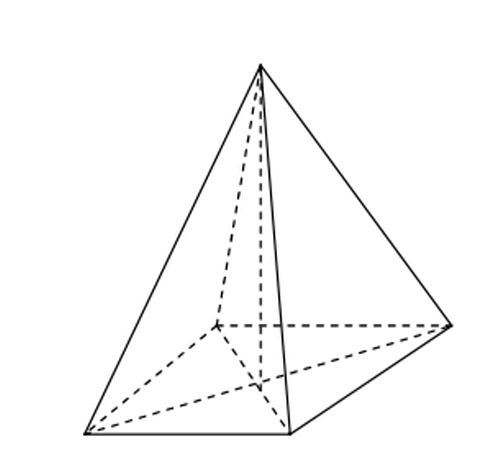
Chứng minh rằng hình chóp tứ giác đều đem những cạnh vày nhau?
Để chứng tỏ rằng hình chóp tứ giác đều đem những cạnh đều bằng nhau, tớ cần dùng những fake thiết và những ấn định lý tương quan cho tới hình chóp tứ giác đều.
1. Giả thiết: Hình chóp tứ giác đều phải sở hữu lòng là hình vuông vắn.
2. Định lý 1: Trong hình chóp tứ giác đều, lối cao của chóp trải qua tâm lòng (giao của 2 lối chéo cánh hình vuông).
3. Định lý 2: Hình tứ giác đều phải sở hữu những cạnh đều bằng nhau.
Bây giờ tất cả chúng ta tiếp tục chứng tỏ.
Ta xét hình chóp tứ giác đều ABCDE. Đáy ABCD là hình vuông vắn và đỉnh E phía trên lối cao của hình vuông vắn. Gọi M là trung điểm của đoạn trực tiếp AE.
Ta có:
- Hình vuông ABCD đem 4 cạnh đều bằng nhau, vì thế là hình vuông vắn.
- Hình tam giác CEM và DEM đều là tam giác cân nặng, vì thế M trung điểm của AE nên CE = ME và DE = ME.
- Có CM = DM, vì thế lối cao EM trải qua tâm lòng ABCD.
Tiếp theo dõi, tớ tiếp tục chứng tỏ rằng những cạnh của tam giác EMN đều đều bằng nhau.
- Do EM = ME (do M là trung điểm của AE).
- Ta cũng có thể có NM = NM (do là cạnh chung).
Do bại liệt, tam giác EMN là tam giác đều.
Vậy, tớ tiếp tục chứng tỏ được rằng hình chóp tứ giác đều đem những cạnh đều bằng nhau.
TOÁN 12 - HÌNH CHÓP CỤT TỨ GIÁC ĐỀU Bài học tập thú vị của Trạng
Khám đập phá đoạn phim về hình chóp cụt tứ giác đều nhằm dò xét hiểu về những Điểm sáng và đặc thù của chính nó. Video tiếp tục khiến cho bạn nắm rõ công thức đo lường và phần mềm vô thực tiễn, giải quyết và xử lý những yếu tố phức tạp tương quan cho tới hình chóp cụt tứ giác đều.
Định nghĩa góc trong số những cạnh của hình chóp tứ giác đều?
Định nghĩa góc trong số những cạnh của hình chóp tứ giác đều là góc thân thích nhị cạnh mặt mũi của hình chóp tuy nhiên những cạnh này nằm trong xúc tiếp với mặt mũi lòng của hình chóp. Góc này là góc trong số những cạnh mặt mũi của hình chóp và mặt mũi lòng và được đo là góc thân thích nhị mặt mũi phẳng lặng tuy nhiên những cạnh này trực thuộc bại liệt. Khi những cạnh mặt mũi của hình chóp đều, góc trong số những cạnh cũng tiếp tục đều và đem nằm trong độ quý hiếm.
Xem thêm: điểm chuẩn đại học nha trang 2022
Hãy lý giải ý nghĩa sâu sắc và hiệu quả của hình chóp tứ giác đều vô thực tiễn.
Hình chóp tứ giác đều là 1 trong mỗi hình học tập đặc trưng được dùng rộng thoải mái vô thực tiễn. Ý nghĩa và hiệu quả của hình chóp tứ giác đều hoàn toàn có thể được tế bào mô tả như sau:
1. Ý nghĩa của hình chóp tứ giác đều:
- Hình chóp tứ giác đều thể hiện tại sự bằng vận, đồng đều và thích mắt vô hình học tập.
- Được dùng nhằm trình diễn mô tả và tế bào phỏng những dự án công trình phong cách xây dựng phức tạp giống như các tòa ngôi nhà, những dự án công trình thiết kế đem cấu tạo nhiều chiều.
- Là một ví dụ minh triệu chứng mang lại đặc thù đồng đều và thăng bằng vô toán học tập và hình học tập.
2. Công dụng của hình chóp tứ giác đều:
- Trong phong cách xây dựng, hình chóp tứ giác đều được dùng nhằm tạo ra những hình dạng rất dị và thú vị sự lưu ý. Ví dụ, nó hoàn toàn có thể được phần mềm nhằm thực hiện đỉnh của những tòa ngôi nhà cao tầng liền kề, những dự án công trình phong cách xây dựng nổi trội và rất dị.
- Trong technology, hình chóp tứ giác đều được dùng nhằm thiết kế cấu tạo và sườn gầm cho những dự án công trình như cầu, ngọn đèn biển, những phần đường đường cao tốc.
- Hình chóp tứ giác đều cũng khá được dùng vô technology hình đồ họa và design sẽ tạo đi ra những cảm giác đặc trưng và tế bào phỏng những hình dạng không khí phức tạp.
Như vậy, hình chóp tứ giác đều không những ý nghĩa thẩm mỹ và làm đẹp tuy nhiên còn tồn tại phần mềm trong vô số nghành nghề không giống nhau.
_HOOK_
Toán 8 - Chân trời tạo nên - Bài 1: Hình chóp tam giác đều - Hình chóp tứ giác đều (HAY NHẤT)
Bạn mong muốn mày mò vẻ đẹp mắt của hình chóp tam giác đều và cơ hội chân mây sáng sủa tạo? Đừng bỏ qua đoạn phim thú vị về chủ thể này. quý khách sẽ tiến hành tận thưởng xúc cảm thú vị Lúc dò xét hiểu về công thức đo lường và phần mềm của hình chóp tam giác đều.












Bình luận