tính chu vi đường tròn

Cách tính chu vi và diện tích S hình tròn là kỹ năng cơ phiên bản cần thiết mang đến việc giải quyết và xử lý bài xích luyện hình học tập.

Công thức tính chu vi hình trụ, diện tích S hình tròn là nền tảng cần thiết, không những giành riêng cho học viên mà còn phải mang đến những người dân thao tác làm việc tương quan cho tới đo lường và đo lường.

Bạn đang xem: tính chu vi đường tròn

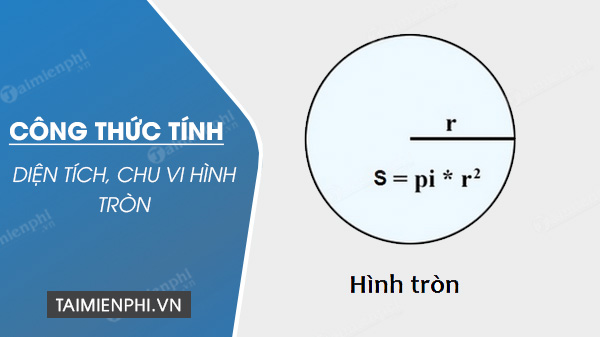
Cách tính chu vi hình trụ và diện tích S hình tròn, sở hữu ví dụ minh họa

Việc học tập và tóm được công thức, phương pháp tính chu vi hình trụ, diện tích S hình tròn tiếp tục tạo nên hiệu suất cao mang đến việc học tập và thao tác làm việc.

Mục Lục bài xích viết:
1. Hình tròn trĩnh.
2. Công thức tính chu vi hình trụ.
3. Công thức tính diện tích S hình trụ.
4. Công thức tính diện tích S hình quạt.
5. Phương pháp học tập công thức tính diện tích S, chu vi hình trụ.
6. Bài luyện tương quan.

Cách tính chu vi hình trụ và diện tích S hình tròn

1. Hình tròn trĩnh là gì?

Hình tròn trĩnh bên trên mặt mày phẳng phiu là điểm bên phía trong lối tròn trĩnh. Chu vi, nửa đường kính và tâm của hình trụ tương quan cho tới lối tròn trĩnh xung quanh. Hình tròn trĩnh hoàn toàn có thể là đóng góp hoặc ngỏ tùy nằm trong nhập việc sở hữu chứa chấp lối tròn trĩnh biên hay là không.

2. Chu vi hình trụ

- Chu vi hình trụ là đường biên giới giới hình trụ, được xem bằng phương pháp nhân 2 lần bán kính với pi hoặc nhân gấp đôi nửa đường kính với pi.

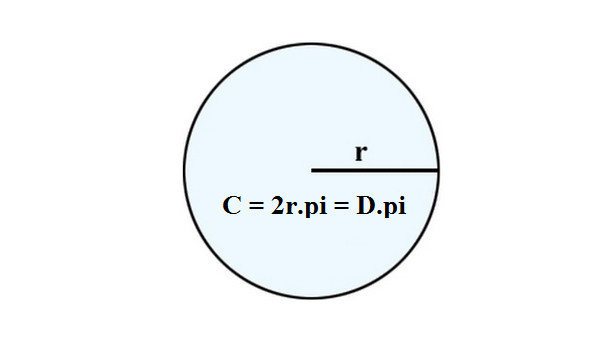
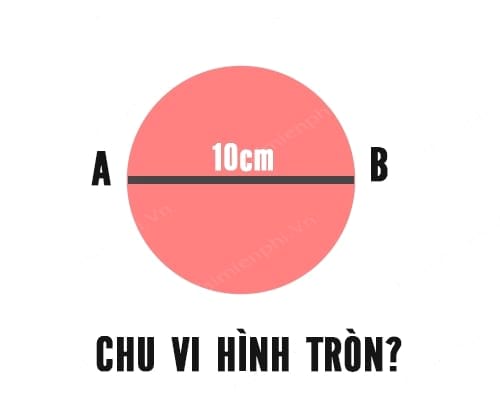
- Ví dụ : Hình tròn trĩnh C sở hữu 2 lần bán kính 10cm. Chu vi hình trụ C là:
C = 10 x Pi = 31,4 centimet.

3. Diện tích hình trụ

- Diện tích hình trụ là phần lắc của hình trụ bên trên mặt phẳng chắc chắn và được xem vị công thức S = Pi x r2.

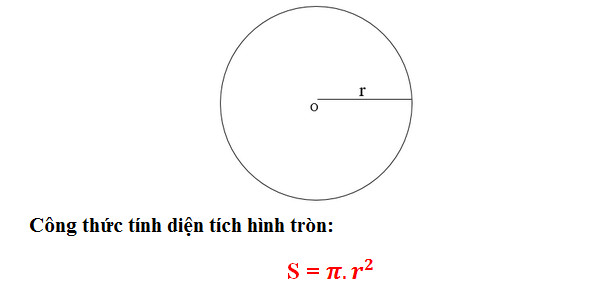
Trong đó:
r : Bán kính hình trụ, vị một nửa 2 lần bán kính (d).
Pi: Số Pi (~3,141...).

- Ví dụ: Hình tròn trĩnh C sở hữu 2 lần bán kính d = 10cm. Diện tích hình trụ C là:
S = Pi x r2 = 3,14 x 52 = 78,5 (cm2).

* Công thức tính diện tích S lối tròn trĩnh lúc biết lối kính: S = Pi x (d/2)2

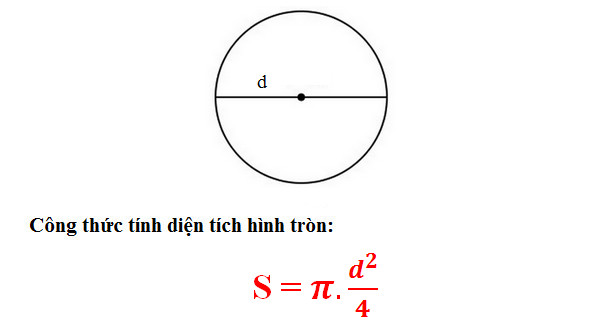
- Trong đó: d là 2 lần bán kính.

- Ví dụ: Hình tròn trĩnh C sở hữu 2 lần bán kính 8cm. Diện tích hình trụ C là:
S = Pi x d2/4 = 50,256 (cm2).

* Công thức tính phụ thuộc vào chu vi hình tròn: S = C2/(4Pi) 

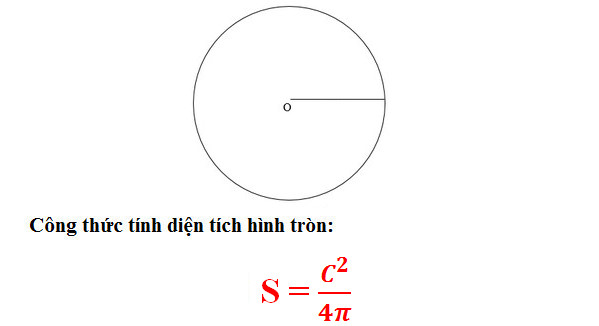
Trong đó: C là chu vi.

Chứng minh công thức:
Ta có: Chu vi hình trụ C = 2Pi.r.
=> r = C/(2Pi).
=> Diện tích hình trụ là: S =C2/(4Pi).

Xem thêm: đạo hàm của căn x

Ví dụ: Cho hình trụ C sở hữu chu vi là 16 cm2. Tính diện tích S hình trụ C.
Giải: Chu vi hình trụ C = 2Pi.r => r = C/(2Pi).
Do cơ, diện tích S hình trụ là S = C2/(4Pi) = đôi mươi,382 (cm2).

* Công thức tính phụ thuộc vào hình quạt: 

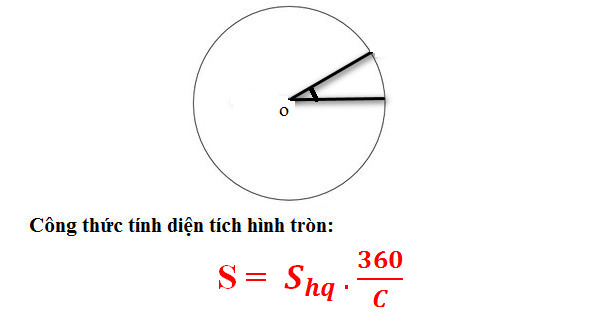
Trong cơ, S: Diện tích toàn phần hình trụ.
Shq: Diện tích hình quạt.
C: Số đo góc ở tâm.

4. Công thức tính diện tích S hình quạt tròn

Trong hình trụ nửa đường kính R, diện tích S hình trụ n được xem bám theo công thức là:

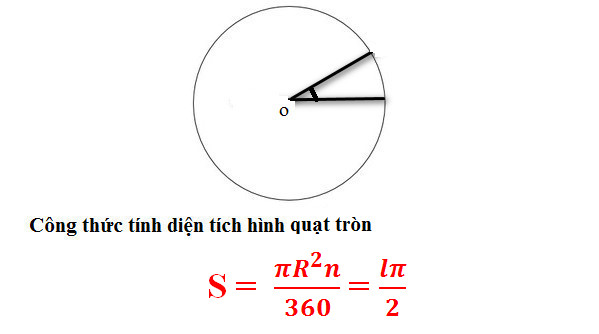
Trong cơ,

- n là góc của hình quạt tròn trĩnh.
- l là chừng lâu năm cung n nhập hình quạt.

5. Phương pháp ghi nhớ công thức, phương pháp tính diện tích S, chu vi hình tròn

- Khi học tập công thức xong xuôi hao hao phương pháp tính, hãy áp dụng nhập thực hiện bài xích luyện nhằm ghi ghi nhớ công thức và nắm rõ thực chất yếu tố. 
- Hình như, bạn cũng có thể học tập công thức trải qua thơ:

Hình tròn trĩnh diện tích S đơn giản
Bình phương nửa đường kính nhân tức thì vào
Ba phảy mươi tứ bề sau
Chu vi cũng dễ dàng tính mau chúng ta à
Đường kính nhân ra
Ba phảy mươi tứ, thế là đang được xong xuôi. 

6. Bài thói quen diện tích S, chu vi hình tròn

Bài luyện 1: Cho hình trụ C sở hữu diện tích S vị 26 cm2. Tính chu vi hình trụ.

Bài giải: 

- Diện tích hình trụ là S = Pi.r2
Mà diện tích S vị 26 cm2 => r = 2,877cm
- Chu vi hình trụ là C = d.Pi = 2r.Pi = 2 . 2,887 . 3,14 = 18,068 (cm)
Vậy chu vi của hình trụ vị 18,068cm.

Bài luyện 2: Tính diện tích S hình trụ, lúc biết chu vi C vị 15,33cm.

Bài giải:

- Ta sở hữu, chu vi hình tròn  C = d.Pi = 2r.Pi => r = C/(2Pi)
- Diện tích hình trụ là S = Pi.r2
=> S = Pi. (C/2Pi)2  =   18,71 (cm2).
Vậy diện tích S hình trụ là 18,71 (cm2).

Công thức tính diện tích S hình trụ và chu vi hình trụ hoàn toàn có thể dùng hoạt bát mang đến nhiều mô hình, kể từ giản dị và đơn giản cho tới phức tạp. Điều xứng đáng để ý, bọn chúng cũng vận dụng nhập câu hỏi phú nhau body tam giác và hình trụ. Việc tính diện tích S tam giác hoặc chu vi trước cơ chung xác lập những độ quý hiếm không giống một cơ hội thuận tiện.

Hy vọng kỹ năng về công thức, phương pháp tính chu vi hình trụ và diện tích S hình trụ tiếp tục tương hỗ độc giả nhập giải quyết và xử lý phong phú câu hỏi.

Trong hình tứ giác, hình bình hành đặc trưng với những đặc điểm đặc thù như 2 cặp góc đối vị, cạnh đối tuy vậy tuy vậy, và lối chéo cánh hạn chế nhau bên trên trung điểm từng lối. kề dụng những đặc điểm này, tất cả chúng ta hoàn toàn có thể đơn giản tính diện tích S và chu vi hình bình hành.

Công thức tính chu vi và diện tích S hình cung cấp nguyệt cũng chính là kỹ năng cần thiết, hữu ích mang đến việc giải những bài xích luyện thực tiễn.

Xem thêm: chức năng của thị trường

Xem thêm: Bài ghi chép về công thức tính chu vi và diện tích S hình cung cấp nguyệt

Chúc chúng ta đạt được thành công xuất sắc.

Khi nắm rõ kỹ năng về tam giác, việc đo lường chu vi tam giác sẽ hỗ trợ học viên giải quyết và xử lý câu hỏi hình học tập một cơ hội thuận tiện.