Viết phương trình đường thẳng đi qua 2 điểm

Phương trình đường thẳng liền mạch trải qua 2 điểm

Chắc hẳn chúng ta học viên đang được gặp gỡ thật nhiều yếu tố về phương trình đường thẳng liền mạch Toán 10: phương trình thông số, phương trình tổng quát mắng của đường thẳng liền mạch là gì? Cách ghi chép phương trình đường thẳng liền mạch trải qua nhị điểm như vậy nào?... đúng không nhỉ ạ? Để giúp cho bạn hiểu hoàn toàn có thể nắm rõ rộng lớn về yếu tố này, VnDoc van nài ra mắt cho tới độc giả tư liệu chỉ dẫn cơ hội xác lập và ghi chép phương trình đường thẳng liền mạch cụ thể chung chúng ta gia tăng kỹ năng và kiến thức, sẵn sàng chất lượng cho những kì ganh đua chuẩn bị tới!

Bạn đang xem: phương trình đường thẳng đi qua 2 điểm

Bản quyền thuộc sở hữu VnDoc.
Nghiêm cấm từng kiểu dáng sao chép nhằm mục tiêu mục tiêu thương nghiệp.

1. Phương trình tổng quát mắng của lối thẳng

Đường trực tiếp Δ với phương trình tổng quát mắng là: $ax + by + c = 0;\left( {{a^2} + {b^2} \ne 0} \right)$ nhận $\overrightarrow n = \left( {a;b} \right)$ thực hiện vectơ pháp tuyến.

2. Phương trình thông số của lối thẳng

- Phương trình thông số của đường thẳng liền mạch trải qua điểm $A\left( {{x_0},{y_0}} \right)$ nhận $\overrightarrow u (a,b)$ thực hiện vecto chỉ phương, Ta có:

$B\left( {x,y} \right) \in d \Leftrightarrow \overrightarrow {AB} = t\overrightarrow u \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x - {x_0} = at} \\ {y - {y_0} = bt} \end{array}} \right.$

$\Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x = {x_0} + at} \\ {y = {y_0} + bt} \end{array}} \right.;\left( {{a^2} + {b^2} \ne 0,t \in \mathbb{R}} \right)$

- Đường trực tiếp d trải qua điểm $A\left( {{x_0},{y_0}} \right)$ , nhận $\overrightarrow u (a,b)$ là vecto chỉ phương, phương trình chủ yếu tắc của đường thẳng liền mạch là $\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b}$ với $(a,b \ne 0)$

3. Cách ghi chép phương trình đường thẳng liền mạch trải qua nhị điểm

a. Sử dụng tấp tểnh nghĩa

Bài toán: Cho nhị điểm A(a, b), B(c, d). Viết phương trình tổng quát mắng của đường thẳng liền mạch d trải qua nhị điểm A và B.

Phương pháp:

Bước 1: Tính: $\overrightarrow {AB} = \left( {c - a;d - b} \right)$ (vectơ chỉ phương của đường thẳng liền mạch d)

Bước 2: Xác tấp tểnh vectơ pháp tuyến của đường thẳng liền mạch d: $\overrightarrow n = \left( {b - d;c - a} \right)$

Bước 3: Phương trình đường thẳng liền mạch d:

$\left( {b - d} \right)\left( {x - a} \right) + \left( {c - a} \right)\left( {y - b} \right) = 0$

b. Sử dụng phương trình tổng quát

Bài toán: Cho nhị điểm A(a, b), B(c, d). Viết phương trình tổng quát mắng của đường thẳng liền mạch d trải qua nhị điểm A và B.

Phương pháp:

Bước 1: Gọi phương trình tổng quát mắng của đường thẳng liền mạch d là hắn = mx + n (*)

Bước 2: Thay tọa chừng A, B vô phương trình tổng quát mắng tao chiếm được hệ phương trình ẩn m, n

$\left\{ {\begin{array}{*{20}{c}} {b = am + n} \\ {d = centimet + n} \end{array}} \right. \Rightarrow \left( {m;n} \right) = \left( {?;?} \right)$

Thay m, n một vừa hai phải tìm kiếm ra vô phương trình (*) tao suy rời khỏi phương trình cần thiết lần.

4. Bài tập dượt ví dụ minh họa

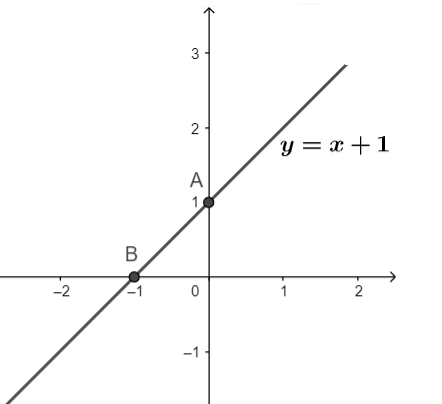
Ví dụ 1: Viết phương trình đường thẳng liền mạch thông số, phương trình tổng quát mắng trải qua 2 điểm A (1;2) và B (2;3). Vẽ đường thẳng liền mạch một vừa hai phải tìm kiếm ra bên trên hệ tọa chừng Oxy.

Hướng dẫn giải

Cách 1: Sử dụng tấp tểnh nghĩa

Cách 2: Sử dụng phương trình tổng quát

$\overrightarrow {AB} = \left( {1,1} \right)$

Phương trình tham ô số: $\frac{{x - 1}}{1} = \frac{{y - 2}}{1}$

$\overrightarrow n = \left( { - 1,1} \right)$

Phương trình tổng quát:

$\begin{matrix} - 1.\left( {x - 1} \right) + 1.\left( {y - 2} \right) = 0 \hfill \\ \Rightarrow hắn = x + 1 \hfill \\ \end{matrix}$

$\overrightarrow {AB} = \left( {1,1} \right)$

Phương trình tham ô số: $\frac{{x - 1}}{1} = \frac{{y - 2}}{1}$

Gọi phương trình tổng quát mắng là:

y = ax + b

Do PTĐT trải qua 2 điểm A, B nên tao có:
$\left\{ {\begin{array}{*{20}{c}} {2 = a.1 + b} \\ {3 = a.2 + b} \end{array}} \right. \Rightarrow \left( {a;b} \right) = \left( {1;1} \right)$

Xem thêm: hợp chất hữu cơ la gì

Vậy PT tổng quát mắng cần thiết lần là: $y = x + 1$

Ví dụ 2: Viết phương trình đường thẳng liền mạch hắn = ax + b biết

a) Đi qua quýt 2 điểm A(-3,2), B (5,-4). Tính diện tích S tam giác được tạo ra bởi đường thẳng liền mạch và 2 trục tọa chừng.

b) Đi qua quýt A (3,1) tuy nhiên song với đường thẳng liền mạch hắn = -2x + m -1

Hướng dẫn giải

a. Gọi phương trình tổng quát mắng là: hắn = ax + b

Do PTĐT trải qua 2 điểm A, B nên tao có:

$\left\{ {\begin{array}{*{20}{c}} {2 = - 3a + b} \\ { - 4 = 5a + b} \end{array}} \right. \Rightarrow \left( {a;b} \right) = \left( { - \frac{3}{4}; - \frac{1}{4}} \right)$

Vậy PT tổng quát mắng cần thiết lần là: $y = - \frac{3}{4}x - \frac{1}{4}$

Giao điểm của đường thẳng liền mạch với trục Ox là: $y = 0 \Rightarrow x = - \frac{1}{3} \Rightarrow A\left( { - \frac{1}{3};0} \right)$

$\Rightarrow \overrightarrow {OA} = \left( { - \frac{1}{3};0} \right) \Rightarrow \left| {\overrightarrow {OA} } \right| = \frac{1}{3}$

Giao điểm của đường thẳng liền mạch với trục Oy là: $x = 0 \Rightarrow hắn = - \frac{1}{4} \Rightarrow B\left( {0; - \frac{1}{4}} \right)$

$\Rightarrow \overrightarrow {OB} = \left( {0; - \frac{1}{4}} \right) \Rightarrow \left| {\overrightarrow {OB} } \right| = \frac{1}{4}$

$\Rightarrow {S_{OAB}} = \frac{1}{2}.OA.OB = \frac{1}{2}.\frac{1}{3}.\frac{1}{4} = \frac{1}{{24}}$

b. Gọi phương trình tổng quát mắng là: hắn = ax + b

Do đường thẳng liền mạch tuy nhiên song với hắn = -2x + m -1

⇒ a = -2

Phương trình đường thẳng liền mạch trở nên hắn = -2x + b

Mà đường thẳng liền mạch qua quýt điểm A(3; 1)

⇒ 1 = 3.(-2) + b
⇒ b = 7

Vậy phương trình tổng quát mắng là: hắn = -2x + 7

Ví dụ 3: Tìm m nhằm đường thẳng liền mạch trải qua nhị điểm đặc biệt trị của thiết bị thị hàm số hắn = 2x³ + 3(m - 1)x² + 6(m - 2)x - 1 tuy nhiên song với đường thẳng liền mạch hắn = -4x + 1.

Lời giải

Ta với y' = 6x² + 6(m - 1)x + 6(m - 2)

Hàm số với đặc biệt trị ⇔ y' = 0 với 2 nghiệm phân biệt

⇔ Δ' > 0 ⇔ 9(m - 1)² - 36(m - 2) > 0 ⇔ 9(m - 3)² > 0 ⇔ m ≠ 3

Thực hiện tại quy tắc phân chia hắn cho tới y' tao với phương trình đường thẳng đi qua 2 điểm đặc biệt trị là:

d: hắn = (-m2 + 6m - 9)x - m² + 3m - 3

Khi cơ d tuy nhiên song với đường thẳng liền mạch hắn = -4x + 1

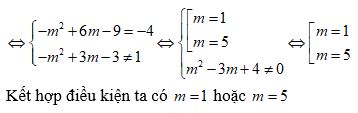
Viết phương trình đường thẳng đi qua 2 điểm

Xem thêm: kim đồng hồ tích tắc tích tắc

-----------------------------------------------------------------------

Trên phía trên VnDoc tiếp tục ra mắt cho tới chúng ta bài xích Viết phương trình đường thẳng liền mạch Toán 10. Bài ghi chép tiếp tục gửi cho tới độc giả những tư liệu tương quan về phương trình đường thẳng liền mạch. Hi vọng qua quýt nội dung bài viết này độc giả đạt thêm tư liệu có ích nhé.

Mời chúng ta nằm trong xem thêm tăng tư liệu tiếp thu kiến thức những môn: